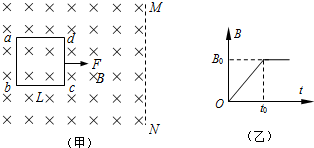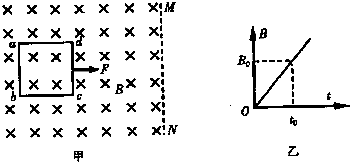题目内容

如图甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着磁场边界，t=O时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，在t0时刻穿出磁场；图乙为外力F随时间变化的图象，若线框质量为m、电阻为R，图象中的F、t0 也为已知量，则在穿出磁场时的速度V=______，匀强磁场的磁感强度B=______．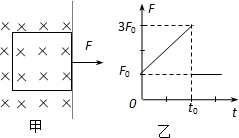
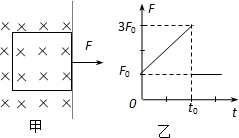
精英家教网
（1）t=0时刻，线框的速度为零，线框没有感应电流，不受安培力，加速度为a=
F0
m
 ①
线框的边长为  L=
1
2
at02=
F0t02
2m

线框刚出磁场时的速度为 v=at0=
F0t0
m
  ②此时线框所受的安培力为FA=BIL，I=
BLv
R

则得 FA=
B2L2v
R
     ③
根据牛顿第二定律得 F-FA=ma       ④
①②③④联立得：B=
2Rm
L2t0
练习册系列答案
相关题目
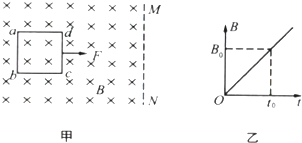（2013?厦门一模）如图甲所示，一正方形单匝线框abcd放在光滑绝缘水平面上，线框边长为L、质量为m、电阻为R，该处空间存在一方向垂直纸面向里的匀强磁场，其右边界MN平行于ab，磁感应强度B随时间t变化的规律如图乙所示，已知
t
 
0
时刻B=
B
 
0
．问：
（1）若线框保持静止，则在时间
t
 
0
内产生的焦耳热为多少？
（2）若线框从零时刻起，在一水平拉力作用下由静止开始做匀加速直线运动，加速度大小为a，经过时间
t
 
0
线框cd边刚要离开边界MN，则在此过程中拉力做的功为多少？（设线框中产生的感应电流大小为I）
王怡同学解法：由匀加速直线运动规律，经过时间
t
 
0
线框的位移为s=
1
2
a
t
2
0
；由牛顿第二定律：F-
B
 
0
IL=ma；所以W=Fs=
1
2
m
a
2
 
t
2
0
+
1
2
B
 
0
ILa
t
2
0
．你认为王怡同学的解法是否正确，若不正确，请你写出正确的解法．
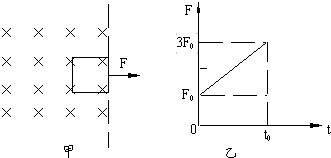（2007?盐城一模）如图甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着边界．t=0时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，经过时间t0穿出磁场．图乙所示为外力F随时间t变化的图象．若线框质量为m、电阻R及图象中的F0、t0均为已知量，则根据上述条件，请你推出：
（1）磁感应强度B的表达式；
（2）线框左边刚离开磁场前瞬间的感应电动势E的表达式．
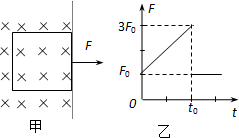精英家教网如图甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着磁场边界，t=O时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动在t0时刻穿出磁场；图乙为外力F随时间变化的图象，若线框质量为m、电阻为R，图象中的F0、t0均为已知量，试求：
（1）正方形金属线框的加速度a的表达式．
（2）正方形金属线框的边长l的表达式
（3）磁感应强度B的表达式．　
（4）从线框开始运动到线框左边刚离开磁场这个过程中线框的平均电流
.
I
的表达式．
如图甲所示，一正方形单匝线框abcd放在光滑绝缘水平面上，线框边长为L、质量为m、电阻为R．该处空间存在一方向竖直向下的匀强磁场，其右边界MN平行于ab，磁感应强度B随时间t变化的规律如图乙所示，0～t0时间内B随时间t均匀变化，t0时间后保持B=B0不变．
精英家教网
（1）若线框保持静止，则在时间t0内产生的焦耳热为多少？
（2）若线框从零时刻起，在一水平拉力作用下由静止开始做匀加速直线运动，加速度大小为a，经过时间t0线框cd边刚要离开边界MN．则在此过程中拉力做的功为多少？
（3）在（2）的情况下，为使线框在离开磁场的过程中，仍以加速度a做匀加速直线运动，试求线框在离开磁场的过程中水平拉力F随时间t的变化关系．
如图甲所示，一正方形单匝线框abcd放在光滑绝缘水平面上，线框边长为L、质量为m、电阻为R；该处空间存在一方向竖直向下的匀强磁场，其右边界MN平行于ab，磁感应强度B随时间t变化的规律如图乙所示，已知t0时刻B=Bo．求：
精英家教网
（1）若线框保持静止，则在时间t0内线框中产生的感应电流大小、方向；
（2）若线框从零时刻起，在一水平拉力作用下由静止开始做匀加速直线运动，加速度大小为a，经过时间to线框cd边刚要离开边界MN；则在0～t0时间内，拉力做的功为多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网