题目内容
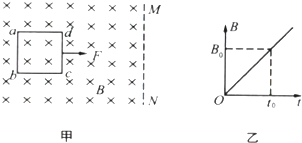 (2013?厦门一模)如图甲所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻为R,该处空间存在一方向垂直纸面向里的匀强磁场,其右边界MN平行于ab,磁感应强度B随时间t变化的规律如图乙所示,已知
(2013?厦门一模)如图甲所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻为R,该处空间存在一方向垂直纸面向里的匀强磁场,其右边界MN平行于ab,磁感应强度B随时间t变化的规律如图乙所示,已知| t | 0 |
| B | 0 |
(1)若线框保持静止,则在时间
| t | 0 |
(2)若线框从零时刻起,在一水平拉力作用下由静止开始做匀加速直线运动,加速度大小为a,经过时间
| t | 0 |
王怡同学解法:由匀加速直线运动规律,经过时间
| t | 0 |
| 1 |
| 2 |
| t | 2 0 |
| B | 0 |
| 1 |
| 2 |
| a | 2 |
| t | 2 0 |
| 1 |
| 2 |
| B | 0 |
| t | 2 0 |
分析:(1)若线框保持静止,在时间
内B均匀增大,穿过线框的磁通量均匀增大,产生恒定的感应电流,根据法拉第电磁感应定律和欧姆定律求出感应电流,由焦耳定律求解焦耳热.
(2)线框处在匀强磁场中所受的安培力的合力为零,根据运动学公式和牛顿第二定律结合求解F,由功的计算公式W=Fs求W.
| t | 0 |
(2)线框处在匀强磁场中所受的安培力的合力为零,根据运动学公式和牛顿第二定律结合求解F,由功的计算公式W=Fs求W.
解答:解:(1)线框中产生的感应电动势 E=
=
,
感应电流为 I=
=
.
故在时间
内产生的焦耳热为Q=I2Rt0=
(2)王怡同学解法不正确.
正确解法:由匀速直线运动规律,经过时间t0线框的位移 s=
a
线框处在匀强磁场中所受的安培力的合力为零,则根据牛顿第二定律得;F=ma,
所以W=Fs=
ma2
答:
(1)若线框保持静止,则在时间
内产生的焦耳热为
.
(2)王怡同学的解法不正确,正确解法见上.
| △φ |
| △t |
| L2B0 |
| t0 |
感应电流为 I=
| E |
| R |
| L2B0 |
| Rt0 |
故在时间
| t | 0 |
L4
| ||
| Rt0 |
(2)王怡同学解法不正确.
正确解法:由匀速直线运动规律,经过时间t0线框的位移 s=
| 1 |
| 2 |
| t | 2 0 |
线框处在匀强磁场中所受的安培力的合力为零,则根据牛顿第二定律得;F=ma,
所以W=Fs=
| 1 |
| 2 |
| t | 2 0 |
答:
(1)若线框保持静止,则在时间
| t | 0 |
L4
| ||
| Rt0 |
(2)王怡同学的解法不正确,正确解法见上.
点评:本题是电磁感应与电路知识、运动学规律和牛顿第二定律的综合应用,比较简单.

练习册系列答案
相关题目
 (2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( )
(2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( ) (2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
(2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( ) (2013?厦门一模)下列四幅图的有关说法中正确的是( )
(2013?厦门一模)下列四幅图的有关说法中正确的是( ) (2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )
(2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )