��Ŀ����
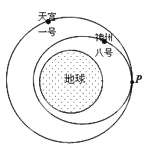
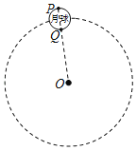
����Ŀ��������ת����T�����Ƶ���������Բ���˶��Ĺ�ת������ͬ���������϶��ĺ��������ڽ��¹��������뾶����Ϊ����뾶��������Բ���˶�������ΪT0����ͼ��ʾ��PQΪ����ֱ����ijʱ��Q�������O�������P��Q��O���ߣ����������������ٶ�Ϊg0��������������ΪG��������
A. ������ܶ�Ϊ��=![]()
B. ����ĵ�һ�����ٶ�![]()
C. ��ͼʾλ�ÿ�ʼ��ʱ����![]() ��P�������O�������
��P�������O�������
D. Ҫʹ���϶��ĺ�������������ı���P����½������ǰ����
���𰸡�B
��������
�����������϶��ĺ��������ڽ��¹��������Բ���˶�������뾶��������뾶R���������������ṩ��������![]() ����ã�
����ã�![]() ����������Ϊ��
����������Ϊ��![]() ��������ܶ�Ϊ��
��������ܶ�Ϊ��![]() ����A������
����A������![]() ���ɵ�����İ뾶Ϊ��
���ɵ�����İ뾶Ϊ��![]() ������
������![]() ���ɵ�����ĵ�һ�����ٶ�Ϊ��
���ɵ�����ĵ�һ�����ٶ�Ϊ��![]() ����B��ȷ��������ת����T�����Ƶ�������Բ���˶��Ĺ�ת������ͬ���پ�
����B��ȷ��������ת����T�����Ƶ�������Բ���˶��Ĺ�ת������ͬ���پ�![]() ʱ��P�������O��Զ����C����Ҫʹ���϶��ĺ�������������ı���P����½������٣�ʹ�����������������������������˶�����D��������B��ȷ��ACD����
ʱ��P�������O��Զ����C����Ҫʹ���϶��ĺ�������������ı���P����½������٣�ʹ�����������������������������˶�����D��������B��ȷ��ACD����

 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�����Ŀ��ijͬѧ����ͼ����ʾװ����̽�������͵����쳤��ϵ��ʵ�飮���Ȳ����������ʱ�����¶�ָ����ָ�ı�߿̶ȣ�Ȼ���ڵ����¶˹������룬������������룬���ָ����ָ�ı�߿̶ȣ�����������������������ٶ�gȡ9.8m/s2��
��������m/102g | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 |
��߿̶�x/10��2m | 15.00 | 18.94 | 22.82 | 26.78 | 30.66 | 34.60 | 42.00 | 54.50 |
��1�������������ݣ���ͼ������������ָ����ָ�ı�߿̶�x����������m�Ĺ�ϵ����_____��
��2����������õ����ݺ�ϵ���߿��жϣ���_____ N��Χ�ڵ�����С�뵯���쳤��ϵ������˶��ɣ����ֹ��ĵ��ɾ���ϵ��Ϊ_____N/m��