题目内容
20.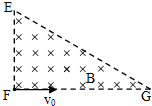 如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )
如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )| A. | 若粒子能到达EG边界,则粒子速度越大,从F运动到EG边的时间越长 | |
| B. | 无论v0取何值,粒子都无法到达E点 | |
| C. | 能到达EF边界的所有粒子所用的时间均相等 | |
| D. | 粒子从F运动到EG边所用的最长时间为$\frac{5πm}{12qB}$ |
分析 粒子从EG边界射出的临界情况是轨迹与EG相切,此时从EG边射出时间最长,根据圆心角,结合周期公式求出最长时间.粒子从EF边界射出粒子运动的轨迹为半圆,通过圆心角比较运动的时间.
解答 解:A、当粒子运动的轨迹与EG边相切时,根据几何关系得,$\frac{r}{cos30°+r}=EF$,解得粒子的轨道半径r=$\frac{EF}{1+\frac{2\sqrt{3}}{3}}$,当半径超过该值时,粒子会从EG边射出,速度越大,半径越大,回旋角越小(因为弦与EF夹角越大),时间越短(周期与速度无关),故A错误.
B、当粒子速度v0=$\frac{qBr}{m}$时,粒子轨迹与EG相切,若粒子速度大于v0,粒子会从EG边出界,若粒子速度小于v0,粒子会从EF边出界,无法到达E点,故B正确.
C、能从EF边出射的粒子都做半圆周运动,因为粒子的周期与速度无关,所以能到达EF边界的所有粒子所用的时间均相等.故C正确.
D、当v0=$\frac{qBr}{m}$时,粒子轨迹与EG相切,此时回旋角最大为150°,时间最长为t=$\frac{5}{12}T=\frac{5πm}{6qB}$.故D错误.
故选:BC.
点评 本题考查带电粒子在磁场中运动,涉及洛仑兹力的计算,圆周运动动力学计算,左手定则,时间计算和临界分析等.关键作出粒子的运动轨迹,结合半径公式和周期公式进行求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.2012年8月2日,伦敦奥运会乒乓球男单决赛在两名中国队员张继科和王皓之间进行,最终张继科以4比1战胜王皓夺冠.关于乒乓球的运动,下列说法正确的是( )
| A. | 研究击球的瞬间球的形变时可以把球看作质点 | |
| B. | 研究球的飞行路线时不能把球看作质点 | |
| C. | 研究球飞行时的旋转时可把球看作质点 | |
| D. | 研究球在空中飞行的时间时可把球看作质点 |
17.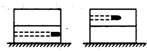 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )| A. | 子弹的末速度大小相等 | B. | 系统产生的热量一样多 | ||
| C. | 子弹对滑块做的功相同 | D. | 子弹和滑块间的水平作用力一样大 |
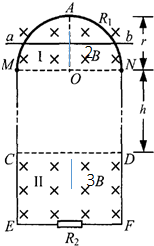 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁场I的磁感应强度大小为2B;磁场II的磁感应强度为3B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止开始下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,平行轨道足够长.已知导体棒ab下落$\frac{r}{2}$时的速度大小为v1,下落到MN处的速度大小为v2.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁场I的磁感应强度大小为2B;磁场II的磁感应强度为3B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止开始下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,平行轨道足够长.已知导体棒ab下落$\frac{r}{2}$时的速度大小为v1,下落到MN处的速度大小为v2. 如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道),若已知一个极地卫星从北纬30°的正上方,按图示方向(逆时针方向)第一次运行至南纬60°正上方时所用时间为t,地球半径为R(地球可看做均匀球体),地球表面的重力加速度为g,不考虑地球的自转,引力常量为G,求:
如图所示,极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道),若已知一个极地卫星从北纬30°的正上方,按图示方向(逆时针方向)第一次运行至南纬60°正上方时所用时间为t,地球半径为R(地球可看做均匀球体),地球表面的重力加速度为g,不考虑地球的自转,引力常量为G,求: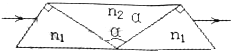 两块相同的直角棱镜与一块等腰棱镜拼接成如图所示的组合棱镜,称为直视棱镜.在主截面内,与底面平行的光线由左方射入棱镜,光线等高地从右面棱镜平行射出,犹如棱镜不存在一样.已知直角棱镜的折射率为n1=$\sqrt{2}$,等腰棱镜的折射率为n2=$\sqrt{3}$,不考虑底面的发射,求等腰棱镜的顶角α.(当光以入射角θ1从折射率为n1的介质入射到折射率为n2的介质中时,折射角为θ2,则它们满足关系式n1•sinθ1=n2•sinθ2)
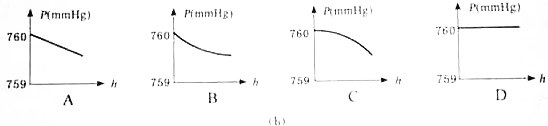
两块相同的直角棱镜与一块等腰棱镜拼接成如图所示的组合棱镜,称为直视棱镜.在主截面内,与底面平行的光线由左方射入棱镜,光线等高地从右面棱镜平行射出,犹如棱镜不存在一样.已知直角棱镜的折射率为n1=$\sqrt{2}$,等腰棱镜的折射率为n2=$\sqrt{3}$,不考虑底面的发射,求等腰棱镜的顶角α.(当光以入射角θ1从折射率为n1的介质入射到折射率为n2的介质中时,折射角为θ2,则它们满足关系式n1•sinθ1=n2•sinθ2) 为了演示大气压随高度而变化的现象,某同学采用了如图所示的装置,图中A为保温瓶(容积为2.5L),B为橡皮塞,C为长约30cm的直角转弯玻璃管(横截面积为0.125cm2),d是一小段有颜色的水柱,手持保温瓶,尽量让玻璃管保持水平,当人由下蹲变为站立再将双手举起的过程中,管中水柱会有比较明显外移,从而显示了大气压随高度而变化的现象.
为了演示大气压随高度而变化的现象,某同学采用了如图所示的装置,图中A为保温瓶(容积为2.5L),B为橡皮塞,C为长约30cm的直角转弯玻璃管(横截面积为0.125cm2),d是一小段有颜色的水柱,手持保温瓶,尽量让玻璃管保持水平,当人由下蹲变为站立再将双手举起的过程中,管中水柱会有比较明显外移,从而显示了大气压随高度而变化的现象.