题目内容
7. 如图所示,磁感应强度为B的匀强磁场中,有一根折成45°角的金属线POQ,其所在平面与磁场垂直,长直导线MN与金属线紧密接触,起始时Ob=L0,且MN⊥OQ,MN在外力的作用下以速度v匀速向右运动,设所有导线单位长度的电阻均为r,求:
如图所示,磁感应强度为B的匀强磁场中,有一根折成45°角的金属线POQ,其所在平面与磁场垂直,长直导线MN与金属线紧密接触,起始时Ob=L0,且MN⊥OQ,MN在外力的作用下以速度v匀速向右运动,设所有导线单位长度的电阻均为r,求:(1)当MN刚开始向右匀速滑动时,闭合电路aOb中感应电流的大小和方向;
(2)驱使MN做匀速运动的外力随时间变化的规律;
(3)导线上产生的热功率随时间变化的规律.
分析 (1)由E=BLv求出感应电动势,由电阻定律求出电路总电阻,然后由欧姆定律求出电流大小,应用右手定则判断出电流方向.
(2)由匀速运动的位移时间公式x=vt求解经过时间t导线离开o点的长度.MN切割磁感线的有效长度就是与MN与轨道接触的两点间的长度,由几何关系求解.由数学知识求得回路的总长,得到总电阻,可由闭合电路欧姆定律求解感应电流的大小.则可确定外力的变化情况.
(3)金属棒匀速运动时,外力的功率等于回路总的电功率,由功率公式P=I2R求出热功率.
解答 解:(1)切割磁感线的有效长度:L=L0tan45°=L0,
感应电动势:E=BL0v,
闭合回路的总电阻:R=(L0+L0tan45°+$\frac{{L}_{0}}{cos45°}$)r=(2+$\sqrt{2}$)L0r,
电路电流:I=$\frac{E}{R}$=$\frac{B{L}_{0}v}{(2+\sqrt{2}){L}_{0}r}$=$\frac{Bv}{(2+\sqrt{2})r}$;
由右手定则可知,感应电流沿逆时针方向;
(2)因导线MN匀速运动,则经过时间t导线离开o点的长度是 x=L0+vt,
MN切割磁感线的有效长度是 L=(L0+vt)tan45°=L0+vt.
t时刻回路中导线MN产生的感应电动势为 E=BLv=B(L0+vt)v,
回路的总电阻为 R=[(L0+vt)+(L0+vt)tan45°+$\frac{{L}_{0}+vt}{cos45°}$]r=(2+$\sqrt{2}$)(L0+vt)r,
感应电流:I=$\frac{E}{R}$=$\frac{B({L}_{0}+vt)v}{(2+\sqrt{2}){(L}_{0}+vt)r}$=$\frac{Bv}{(2+\sqrt{2})r}$
MN受到的安培力:F安培=BIL=$\frac{{B}^{2}({L}_{0}+vt)^{\;}v}{(2+\sqrt{2})r}$,
MN做匀速直线运动,处于平衡状态,由平衡条件得:
拉力:F=F安培=$\frac{{B}^{2}({L}_{0}+vt)^{\;}v}{(2+\sqrt{2})r}$;
(3)导线上产生的热功率:P=I2R=$\frac{{B}^{2}{v}^{2}({L}_{0}+vt)}{(2+\sqrt{2})r}$;
答:(1)当MN刚开始向右匀速滑动时,闭合电路aOb中感应电流的大小为$\frac{Bv}{(2+\sqrt{2})r}$,方向:沿逆时针方向;
(2)驱使MN做匀速运动的外力随时间变化的规律为:F=$\frac{{B}^{2}({L}_{0}+vt)^{\;}v}{(2+\sqrt{2})r}$;
(3)导线上产生的热功率随时间变化的规律为:P=$\frac{{B}^{2}{v}^{2}({L}_{0}+vt)}{(2+\sqrt{2})r}$.
点评 本题考查了求电流、判断电流方向、求力、求热功率等问题,是一道电磁感应与电学、力学相结合的综合题,应用E=BLv、电阻定律、欧姆定律、安培力公式、平衡条件、电功率公式可以解题,本题有一定难度.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{n}$F | B. | F | C. | nF | D. | n2F |
| A. | 匀速下降运动 | B. | 匀速上升运动 | C. | 加速下降运动 | D. | 加速上升运动 |
| A. | 飞船绕地球运行的周期将增大 | B. | 飞船所受到的向心力将减小 | ||
| C. | 飞船的向心加速度将增大 | D. | 飞船绕地球运行的速率将增大 |
 如图所示是高速公路旁的交通标志,图中的“100”表示小汽车必须限制在100km/h内行驶,“杭州 88km”表示到杭州还有88km.“100km/h”和“88km”分别指( )
如图所示是高速公路旁的交通标志,图中的“100”表示小汽车必须限制在100km/h内行驶,“杭州 88km”表示到杭州还有88km.“100km/h”和“88km”分别指( )| A. | 瞬时速度,位移 | B. | 瞬时速度,路程 | C. | 平均速度,位移 | D. | 平均速度,路程 |
| A. | 10N | B. | 15N | C. | 25N | D. | 30N |
| A. | 卫星运行的轨道半径越大,速度越小,运行周期越大 | |
| B. | 国家正在我省文昌市兴建第四个航天发射场.与我国原有的其他航天发射场相比较,文昌在地理位置因素的优势是纬度低.地球自转线速度大 | |
| C. | 人造卫星在升空过程中处于超重状态 | |
| D. | 人造地球同步卫星在赤道上空运行,运行一周所需的时间为一年 |
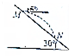 如图所示,从倾角为30°的足够长的斜面上的M点,以初速度v0水平抛出一小球,不计空气阻力,M点到球落地点N之间的距离是$\frac{4{v}_{0}^{2}}{3g}$.
如图所示,从倾角为30°的足够长的斜面上的M点,以初速度v0水平抛出一小球,不计空气阻力,M点到球落地点N之间的距离是$\frac{4{v}_{0}^{2}}{3g}$.