题目内容
用水平拉力拉着滑块沿半径为R的水平圆轨道运动一周,如图所示,已知物块与轨道间动摩擦因数为μ,物块质量为m,求此过程中摩擦力所做的功.

答案:-2μmgπR
解析:
提示:
解析:
|
分析:由题意知,物体受到的摩擦力在整个过程中大小为f=μmg不变,方向时刻变化,是变力,我们可以把圆周分成无数段小微元段,每一小段可近似看成直线,从而摩擦力在每一小段上方向不变,每一小段可用恒力做功的公式计算,然后各段累加起来,便可求得结果,这种思维方法叫做微元法. 解:把圆轨道分成s1、s2、s3……微元段,摩擦力在每一段上为恒力,则在每一段上做的功W1=-μmgs1,W2=-μmgs2,W3=-μmgs3……Wn=-μmgsn. W=w1+w2+w3+……+wn =-μmg(s1+s2+s3+……+sn)=-μmg·2πR 所以滑块运动一周,摩擦力做功为W=-2μmgπR. |
提示:
|
(1)摩擦力做功的计算公式W=Fs,其中s为物体运动的路程. (2)空气阻力和介质阻力大小恒定的情况下,做功的计算与摩擦力做功的计算相同. |

练习册系列答案
相关题目
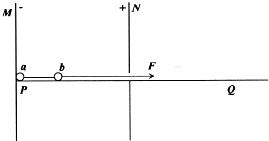 如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的
如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的