题目内容
4.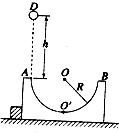 如图所示,一质量为M的半圆形槽内壁光滑,放在光滑的水平面上,槽的左侧有一固定的木桩以阻止槽水平向左运动,槽的半径为R.今从槽左侧A端的正上方D处自由释放一个质量为m的小球,球恰从A点自然进入槽的内壁轨道.为了使小球和沿槽的内壁恰好运动到槽的右端B点,试求D点至A点的高度.
如图所示,一质量为M的半圆形槽内壁光滑,放在光滑的水平面上,槽的左侧有一固定的木桩以阻止槽水平向左运动,槽的半径为R.今从槽左侧A端的正上方D处自由释放一个质量为m的小球,球恰从A点自然进入槽的内壁轨道.为了使小球和沿槽的内壁恰好运动到槽的右端B点,试求D点至A点的高度.
分析 小球从D点至O′点的过程中,半圆形槽由于木桩的阻止,半圆槽静止不动.对于小球,只有重力做功,小球的机械能守恒,求出小球到达半圆槽的最低点O′的速度.当小球从半圆槽的最低点O′运动到B点的过程中,半圆槽由于小球的压力作用离开木桩,以半圆槽和小球组成的系统为研究对象,水平方向动量守恒和机械能守恒,根据两大守恒列出方程,联立求解D点到A点的高度h.
解答 解:设D点至A点的高度为h.小球从D处开始运动至B端的过程,可分为两个阶段:
第一阶段:小球从D点自由下落经A点至最低点O′,设小球经过O′的速度大小为v1.由于只有重力做功,小球的机械能守恒,则得:
mg(h+R)=$\frac{1}{2}$m${v}_{1}^{2}$…①
第二阶段:小球从O′点运动到B点,此时小球和槽有共同速度v2,对槽和小球系统而言,只有重力做功,系统的机械能守恒,可得:
mgR+$\frac{1}{2}$(m+M)${v}_{2}^{2}$=$\frac{1}{2}m{v}_{1}^{2}$…②
该阶段,系统在水平方向不受外力,水平方向动量守恒,取水平方向向右为正方向,由动量守恒定律得:
mv1=(m+M)v2 …③
联立以上三式,解得:h=$\frac{M}{m}$R
答:D点到A点的高度为为$\frac{M}{m}$R.
点评 本题关键是分析物理过程,寻找解题规律是关键.要知道小球从最低点O′上升的过程,系统的水平方向动量守恒,但总的动量并不守恒.

练习册系列答案
相关题目
15.质量相等的两个小球A、B,在光滑的水平面上沿同一直线向同一方向运动,A球初动量为7㎏•m/s,B球初动量为5㎏•m/s,当A球追上B球发生碰撞后,A、B两球动量的可能值为( )
| A. | PA=6㎏•m/s,PB=6㎏•m/s | B. | PA=3㎏•m/s,PB=9㎏•m/s | ||
| C. | PA=-2㎏•m/s,PB=14㎏•m/s | D. | PA=-4㎏•m/s,PB=10㎏•m/s |
12.关于物体的运动,下列说法正确的是( )
| A. | 物体加速度增加,速度一定增加 | |
| B. | 物体速度发生变化,合外力可能没有做功 | |
| C. | 物体做匀速运动,机械能一定守恒 | |
| D. | 物体受一恒力作用,可能做匀速圆周运动 |
9.关于气体压强和热力学定律,以下理解不正确的是( )
| A. | 从微观上讲,气体的压强是大量的气体分子无规则运动不断撞击器壁产生的 | |
| B. | 只从单一热源吸热,使之完全变为有用功而不产生其他影响的机器是可以制造出来的 | |
| C. | 温度升高时,气体的压强一定增大 | |
| D. | 绝对零度不可达到 |
14.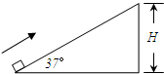 一质量为m的物体以某一速度冲上一个倾角为37°的斜面,其运动的加速度的大小为0.9g,这个物体沿斜面上升的最大高度为H,则在这过程中( )
一质量为m的物体以某一速度冲上一个倾角为37°的斜面,其运动的加速度的大小为0.9g,这个物体沿斜面上升的最大高度为H,则在这过程中( )
 一质量为m的物体以某一速度冲上一个倾角为37°的斜面,其运动的加速度的大小为0.9g,这个物体沿斜面上升的最大高度为H,则在这过程中( )
一质量为m的物体以某一速度冲上一个倾角为37°的斜面,其运动的加速度的大小为0.9g,这个物体沿斜面上升的最大高度为H,则在这过程中( )| A. | 物体的动能减少了0.9mgH | B. | 物体的重力势能增加了0.9mgH | ||
| C. | 物体的动能损失了0.5mgH | D. | 物体的机械能损失了0.5mgH |

 如图所示.水平传送装置由轮半径均为R=$\frac{1}{π}$米的主动轮O1和从动轮O2及传送带等构成.两轮轴心相距L=8.0米,轮与传送带不打滑.现用此装置运送一袋面粉,已知面粉袋与传送带间的动摩擦因数为μ=0.4,这袋面粉中间的面粉可不断地从袋中渗出.
如图所示.水平传送装置由轮半径均为R=$\frac{1}{π}$米的主动轮O1和从动轮O2及传送带等构成.两轮轴心相距L=8.0米,轮与传送带不打滑.现用此装置运送一袋面粉,已知面粉袋与传送带间的动摩擦因数为μ=0.4,这袋面粉中间的面粉可不断地从袋中渗出.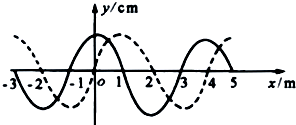 如图所示,实线是一列简谐波在某一时刻的波形图象,虚线是0.2s后它的波形图象,求:
如图所示,实线是一列简谐波在某一时刻的波形图象,虚线是0.2s后它的波形图象,求: