题目内容
15.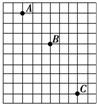 如图所示为一个小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm,如果g取10m/s2,那么:
如图所示为一个小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm,如果g取10m/s2,那么:①闪光频率是10Hz;
②小球运动中水平分速度的大小是1.5m/s.
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直方向上在相等时间内的位移之差是一恒量求出闪光的周期,从而得出闪光的频率.根据水平位移和时间求出平抛运动的初速度.
解答 解:(1)在竖直方向上有:△y=2L=gT2,解得T=$\sqrt{\frac{2L}{g}}=\sqrt{\frac{2×0.05}{10}}=0.1s$.
则照片闪光的频率f=$\frac{1}{T}=\frac{1}{0.1}=10Hz$.
(2)小球平抛运动的初速度${v}_{0}=\frac{x}{T}=\frac{3L}{T}=\frac{0.15}{0.1}=1.5m/s$.
故答案为:(1)10;(2)1.5
点评 解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,运用运动学公式灵活求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )| A. | c点电势为8V | |
| B. | 场强大小为$\frac{4}{{\sqrt{2}L}}$ | |
| C. | 质子从b运动到c,所用的时间为$\frac{2L}{υ_0}$ | |
| D. | 若质子从bd方向入射,它在以后运动中电势能会先减小后增加 |
6.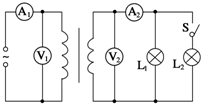 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )| A. | A1示数变小,A1与A2示数的比值不变 | |
| B. | A1示数变大,A1与A2示数的比值变大 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |
3.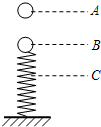 一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
 一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )
一小球自A点由静止自由下落 到B点时与弹簧接触,到C点时弹簧被压缩到最短.若不计弹簧质量和空气阻力,在小球由A-B-C的运动过程中( )| A. | 小球在B点时动能最大 | |
| B. | 小球的重力势能不断增大 | |
| C. | 小球和弹簧组成的系统机械能守恒 | |
| D. | 到C点时小球重力势能的减少量等于弹簧弹性势能的增加量 |
7.地球赤道上的物体随地球自转的向心加速度为a;假设月球绕地球作匀速圆周运动,轨道半径为r1,向心加速度为a1.已知万有引力常量为G,地球半径为R.下列说法中正确的是( )
| A. | 地球质量M=$\frac{a{R}^{2}}{G}$ | B. | 地球密度$ρ=\frac{{3{a_1}r_1^2}}{{4πG{R^3}}}$ | ||
| C. | 地球的第一宇宙速度为$\sqrt{aR}$ | D. | 向心加速度之比$\frac{{a}_{1}}{a}$=$\frac{{R}^{2}}{{{r}_{1}}^{2}}$ |
4.某人站在一星球上,以速度v0竖直向上抛一小球,经t秒后,球落回手中,已知该星球半径为R,现将此球沿此星球表面将小球水平抛出,欲使其不落回星球,则抛出时的速度至少为( )
| A. | $\frac{v_0}{t}$ | B. | $\sqrt{\frac{{{v_0}R}}{t}}$ | C. | $\sqrt{\frac{{2{v_0}R}}{t}}$ | D. | $\sqrt{\frac{v_0}{Rt}}$ |
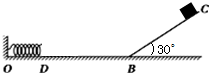 如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计).
如图所示,水平轨道ODB与一斜面BC平滑相交于B点,斜面BC与水平面的夹角为30°,水平轨道OD段光滑,DB段粗糙,DB段长度L=2m,动摩擦因数?=0.1,BC段光滑且长度S=3.6m,轻质弹簧左端固定于O点,弹簧原长时,右端恰好处于D点.现把质量m=2kg的可视为质点的小滑块由C点静止释放,沿CB下滑,进入水平轨道继续滑行后压缩弹簧,设滑块在经过B点瞬间速率大小不变(取g=10m/s2,空气阻力不计).
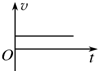
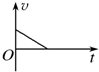
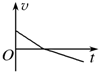
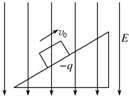 如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )
如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )