��Ŀ����
7����̫������̽���������ɼ��١�ƫת���ռ���������ɣ���ԭ���ɼ����£���ͼ1��ʾ������״�ļ��ٵ糡����߽�Ϊ����ͬ��ƽ�а�Բ���棬Բ��ΪO����Բ����AB�ĵ���Ϊ2�գ��գ�o������Բ����CD�ĵ���Ϊϕ���㹻�����ռ���MNƽ�б߽�ACDB��ACDB��MN��ľ���ΪL������̫����Ư��������Ϊm������Ϊq�Ĵ��������ӣ������ܾ��ȵ�������ABԲ�����ϣ��������ٵ糡�Ӿ�ֹ��ʼ���٣��������Ӽ������ú�������������ӵ�Ӱ�죬�����ǹ��߽�ACDB�������ٴη��أ�
��1�������ӵ���O��ʱ�ٶȵĴ�С��
��2����ͼ2��ʾ����PQ����ACDB�غ����㹻�������ռ���MN֮�������һ����ǿ�ų�������ֱֽ�����ڣ����־���������ABԲ��������Ӿ�O�����ų��������$\frac{2}{3}$�ܴ�MN���ϣ������ӴŸ�Ӧǿ�ȵĴ�С��
��3����ͼ3��ʾ����PQ����ACDB�غ����㹻�������ռ���MN֮�������һ����ֱMN����ǿ�糡���糡ǿ�ȵķ�����ͼ��ʾ����С$E=\frac{ϕ}{4L}$������ABԲ�����ռ�����ij���Ӿ�O�����糡���ռ���MN��O����Զ��������ӵ���O����ٶȵķ��������PQ��MN���˶���ʱ�䣮
���� ��1�����������ڵ糡�м��ٹ��̣��糡�������������ݶ��ܶ��������ӵ���O��ʱ�ٶȵĴ�С��
��2����ABԲ�����ռ�����������$\frac{2}{3}$�ܴ�MN���ϣ��϶˸պ��ܴ�MN�ϵ�������MN���У�����ķ�����OA֮��ļн�Ϊ60�㣬�������ӵ��˶��켣���õ��켣��Բ�Ľǣ����ݼ��ι�ϵ����켣�뾶������ţ�ٵڶ����ɺ�����������ʽ������Ÿ�Ӧǿ�ȣ�
��3�������ڵ糡���˶��Ĺ켣��MN����ʱ���е㵽O��ľ�����Զ�����˶�����ƽ���˶�������̣������˶��ķֽⷨ���ɷ�λ�ƹ�ʽ��ţ�ٵڶ����ɽ�Ͻ��
���  �⣺��1�����������ڵ糡�м���ʱ���糡���������ɶ��ܶ����ã�
�⣺��1�����������ڵ糡�м���ʱ���糡���������ɶ��ܶ����ã�
qU=$\frac{1}{2}m{v}^{2}$-0
�� U=2��-��=��
��� v=$\sqrt{\frac{2q��}{m}}$
��2����ABԲ�����ռ�����������$\frac{2}{3}$�ܴ�MN���ϣ����϶˸պ��ܴ�MN�ϵ�������MN���У�����ķ�����OA֮��ļн�Ϊ60�㣬�ڴų��е��˶��켣��ͼ���켣��Բ�Ľ� ��=60�㣮
���ݼ��ι�ϵ�ɵã�����Բ���˶��Ĺ켣�뾶 R=2L
�����������ṩ�������ã�qvB=m$\frac{{v}^{2}}{R}$
������� B=$\frac{1}{L}$$\sqrt{\frac{m��}{2q}}$
��3����ͼ�������ڵ糡���˶��Ĺ켣��MN����ʱ���е㵽O��ľ�����Զ�����˶�����ƽ���˶�������̣�
������ͼ���꣮��
L=$\frac{1}{2}•\frac{qE}{m}{t}^{2}$
�ɵ� t=$\sqrt{\frac{2mL}{qE}}$=2L$\sqrt{\frac{2m}{q��}}$
vx=$\frac{qE}{m}t$=$\sqrt{\frac{2qEL}{m}}$=$\sqrt{\frac{q��}{2m}}$
���ٶ���x�᷽��ļн�Ϊ��
�� cos��=$\frac{{v}_{x}}{v}$
��� cos��=$\frac{1}{2}$
�ʦ�=60��
��
��1�����ӵ���O��ʱ�ٶȵĴ�С��$\sqrt{\frac{2q��}{m}}$��
��2�����ӴŸ�Ӧǿ�ȵĴ�С��$\frac{1}{L}$$\sqrt{\frac{m��}{2q}}$��
��3�������ӵ���O����ٶȵķ�����x��������ļн�Ϊ60�㣬б�����Ϸ�������PQ��MN���˶���ʱ����2L$\sqrt{\frac{2m}{q��}}$��
���� ���⿼���˴��������ڵ糡�еļ��١��ų��е�ƫת�͵糡ƫת���ؼ��������ӵ��˶��켣����������˼ά�����糡�е�ɵ��˶����⣬ѡ����ʵ���ѧ���ɽ�����⣮


| A�� | �����������Ļ���ͷP����������� | |
| B�� | ��Դ������������ | |
| C�� | ��ֵ����R�����ĵĹ���Ϊ0.5W | |
| D�� | ��Դ��Ч�ʴﵽ���ֵ |
| A�� | ���������ȼ���ֱ���˶�ʱ��v1��v2 | B�� | ���������ȼ���ֱ���˶�ʱ��v1��v2 | ||
| C�� | ������������ֱ���˶�ʱ��v1=v2 | D�� | ������������ֱ���˶�ʱ��v1��v2 |

�ٰ���·ԭ��ͼ��ͼ2ʵ���·����������
��ʵ���вⶨ�����������ݣ�
| I/A | 0.10 | 0.15 | 0.17 | 0.23 | 0.25 | 0.30 |
| U/V | 1.20 | 1.10 | 1.00 | 0.80 | 1.00 | 0.60 |
����I-Uͼ��ó���صĵ綯��Ϊ1.50V������Ϊ0.50����
 ��ͼΪһ�����������˶���v-tͼ����
��ͼΪһ�����������˶���v-tͼ����
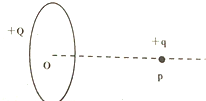 ��ͼ��ʾ��һ���̶���ϸ����ֱ���ã�OΪԲ����Բ�ģ�Բ���İ뾶ΪR��Բ�����о��ȷֲ�+Q�ĵ��������ϸ���������ϣ���Բ����Բ��O���Ϊ$\sqrt{3}$R��P�㴦�̶�һ��+q�ĵ��ɣ���+q�ĵ����ܵ��Ŀ������Ĵ�С�ͷ���
��ͼ��ʾ��һ���̶���ϸ����ֱ���ã�OΪԲ����Բ�ģ�Բ���İ뾶ΪR��Բ�����о��ȷֲ�+Q�ĵ��������ϸ���������ϣ���Բ����Բ��O���Ϊ$\sqrt{3}$R��P�㴦�̶�һ��+q�ĵ��ɣ���+q�ĵ����ܵ��Ŀ������Ĵ�С�ͷ���