题目内容
 一传送带装置示意如图,其中传送带经过AB区域时是水平的,经过BC区域时变为圆弧形(圆弧由光滑模板形成,未画出),经过CD区域时是倾斜的,AB和CD都与BC相切.现有大量的质量均为m=2kg的小工件一个一个在A处以初速为v0=1m/s,方向水平向右滑上传送带,经传送带运送到D处,D和A的高度差为h=2m.传送带以恒定的速率v=2m/s运动,小工件与传送带之间的动摩擦因数μ=0.5,当前一个小工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,每个小工件在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动).这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.求
一传送带装置示意如图,其中传送带经过AB区域时是水平的,经过BC区域时变为圆弧形(圆弧由光滑模板形成,未画出),经过CD区域时是倾斜的,AB和CD都与BC相切.现有大量的质量均为m=2kg的小工件一个一个在A处以初速为v0=1m/s,方向水平向右滑上传送带,经传送带运送到D处,D和A的高度差为h=2m.传送带以恒定的速率v=2m/s运动,小工件与传送带之间的动摩擦因数μ=0.5,当前一个小工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,每个小工件在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动).这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.求(1)CD段相邻两箱的距离L多大?
(2)在1分钟内,共运送小工件的数目N为多少?
(3)在1分钟内,电动机的平均抽出功率
. | P |
分析:(1)工件刚放在水平传送带上进行受力分析,运用牛顿第二定律和运动学公式求解
(2)根据1分钟内传送带前进的距离和CD段相邻两箱的距离求解.
(3)根据能量守恒求出在1分钟内电动机消耗的能量,再求出平均功率.
(2)根据1分钟内传送带前进的距离和CD段相邻两箱的距离求解.
(3)根据能量守恒求出在1分钟内电动机消耗的能量,再求出平均功率.
解答:解:(1)小工件受滑动摩擦力,根据牛顿第二定律得
a=μg=5m/s2
t=
=0.2s
L=vt=2×0.2m=0.4m
(2)1分钟内传送带前进的距离是vt
1分钟内,共运送小工件的数目N=
=300
(3)W=
mv2-
+mgh=43J
△X=vt-(v0t+
at2)=0.1m
Q=μmg△x=1J
P=
=220w
答:(1)CD段相邻两箱的距离是0.4m
(2)在1分钟内,共运送小工件的数目N为300个
(3)在1分钟内,电动机的平均输出功率是220w.
a=μg=5m/s2
t=
| v-v0 |
| a |
L=vt=2×0.2m=0.4m
(2)1分钟内传送带前进的距离是vt
1分钟内,共运送小工件的数目N=
| vT |
| L |
(3)W=
| 1 |
| 2 |
| 1 |
| 2 |
| mv | 2 0 |
△X=vt-(v0t+
| 1 |
| 2 |
Q=μmg△x=1J
P=
| N(W+Q) |
| T |
答:(1)CD段相邻两箱的距离是0.4m
(2)在1分钟内,共运送小工件的数目N为300个
(3)在1分钟内,电动机的平均输出功率是220w.
点评:本题关键分析清楚工件的运动情况,摩擦生热等于滑动摩擦力与相对位移大小的乘积.

练习册系列答案
相关题目
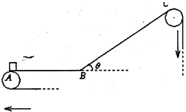 一传送带装置示意如图所示,其中传送带AB区域是水平的,BC区域的倾角θ=37°,B处有一很小段圆弧形过渡(圆弧形长度不计,图中未画出),AB长度为L1=4m,BC长度为L2=16.6m.现将一个质量m=l.0kg的工件(可视为质点)无初速轻放在传送带A端,工件与传送带间动摩擦因素为μ=0.8.设传送带运行的速率v=8.4m/s始终保持不变,取g=10m/s2,sin37°=0.6,cos37°=0.8.
一传送带装置示意如图所示,其中传送带AB区域是水平的,BC区域的倾角θ=37°,B处有一很小段圆弧形过渡(圆弧形长度不计,图中未画出),AB长度为L1=4m,BC长度为L2=16.6m.现将一个质量m=l.0kg的工件(可视为质点)无初速轻放在传送带A端,工件与传送带间动摩擦因素为μ=0.8.设传送带运行的速率v=8.4m/s始终保持不变,取g=10m/s2,sin37°=0.6,cos37°=0.8.
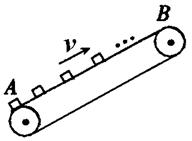
 ,方向水平向右滑上传送带,经传送带运送到D处,D和A的高度差为h=2m。传送带以恒定的速率
,方向水平向右滑上传送带,经传送带运送到D处,D和A的高度差为h=2m。传送带以恒定的速率 运动,小工件与传送带之间的动摩擦因数
运动,小工件与传送带之间的动摩擦因数 ,当前一个小工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,每个小工件在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动)。这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求
,当前一个小工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,每个小工件在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动)。这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求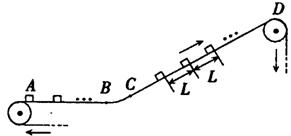
 。
。