Question

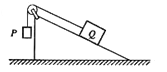
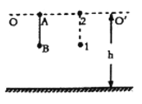
【题目】在探究“ 物体质量一定时加速度与力的关系” 的实验中， 某兴趣小组对教材介绍的实验方案进行了优化， 设计了如图所示的实验装置。 其中 M 为带滑轮的小车的质量， m为砂和砂桶的质量（ 滑轮质量不计）。

(1).依据优化后实验原理图， 该实验______（ 填“需要” 或“ 不需要”） 将带滑轮的长木板右端垫高， 以平衡摩擦力； 实验中______（ 填“ 一定要” 或“ 不必要”） 保证砂和砂桶的质量 m 远小于小车的质量 M；

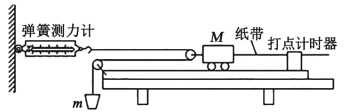
(2).该同学在实验中得到如图(a)所示的一条纸带（ 两计数点间还有四个点没有画出）， 已知打点计时器采用的是频率为 50Hz 的交流电， 根据纸带可求出小车的加速度为____ m/s2（ 结果保留两位有效数字）。

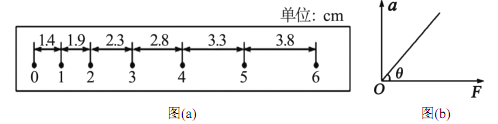
(3).如图(b)所示， 以弹簧测力计的示数 F 为横坐标， 加速度为纵坐标， 画出的 a－F 图象是一条直线， 求得直线的斜率为 k， 则小车的质量为______。

Answer 1

【答案】需要 不必要 0.50

【解析】

（1）只有平衡摩擦力，弹簧秤的拉力的2倍才等于小车的合外力；小车所受拉力可由弹簧测力计测出，实验不需要控制砂和砂桶质量远小于小车质量。

（2）根据匀变速直线运动的推论：△x=at2求出加速度大小。

（3）根据题意，应用牛顿第二定律求出图象的函数表达式，然后分析答题。

(1)依据优化后实验原理图，该实验需要将带滑轮的长木板右端垫高，以平衡摩擦力，这样才能使得弹簧秤的拉力的2倍等于小车的合外力；由于有弹簧测力计测量拉力的大小，则实验中不必要保证砂和砂桶的质量m远小于小车的质量M；

(2) 频率为50Hz，则周期为0.02s，由于两计数点间还有四个点没有画出，相邻计数点的时间间隔为0.1s，由△x=aT2可得：a=m/s2=0.478m/s2。

(3)根据牛顿第二定律：2F=Ma，则a=F，则=k,解得M=。