题目内容
【题目】如图所示,在光滑水平地面上有一质量为m2=4.0kg的平板小车,小车的左端有一固定的圆弧形光滑轨道,轨道足够高.小车右端有一质量为m1=0.9kg的软木块(可视为质点),开始小车和木块均处于静止状态,小车上表面光滑.一质量m0=0.1kg的子弹以v0=20m/s的水平速度向左飞来打到木块内面没有射出,已知作用时间极短.重力加速度g=10m/s2.求:
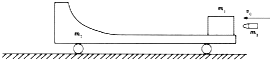
(1)子弹刚打到软木块内后,木块的速度大小;
(2)木块相对小车水平上表面沿圆弧形轨道上升的最大高度.
【答案】(1)2m/s;(2)0.1375m.
【解析】
(1)子弹刚打到软木块的过程,取向左为正方向,由动量守恒定律得:
m0v0=(m0+m1)v1;
解得木块获得的速度为:
v1=2m/s
(2)当木块上升到圆弧轨道的最高点时,木块与小车的速度相同,设为v2,最大高度设为h.根据系统水平方向动量守恒得:
(m0+m1)v1=(m0+m1+m2)v2
根据能量守恒定律得:
![]() (m0+m1)v12=
(m0+m1)v12=![]() (m0+m1+m2)v22+(m0+m1)gh
(m0+m1+m2)v22+(m0+m1)gh
联立解得:
h=0.1375m

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目