题目内容
在光滑水平面上,有A、B两个小球在一条直线上相向运动.已知A球质量ma="2" kg,以速度va="1" m/s向右运动;B球质量mb="4" kg,以速度vb="5" m/s向左运动,碰后A反向,以7 m/s的速度运动.求碰撞后B球的速度.
碰撞后B球速度大小为1 m/s,方向向左
选A、B两球组成的系统为研究对象,它们碰撞过程中,水平方向不受外力作用.根据动量守恒定律有:mAvA+mBvB=mAvA′+mBvB′解得:vB′=vB+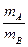 (vA-vA′)
(vA-vA′)
选取向左为正方向(因为已知矢量中向左的较多,这是选正方向的原则),vA="-1" m/s,vB="5" m/s,vA′="7" m/s,代入上式,得碰撞后B球的速度为:
vB′="5" m/s+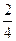 (-1-7) m/s="1" m/s
(-1-7) m/s="1" m/s
即碰撞后B球速度大小为1 m/s,方向向左.
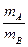 (vA-vA′)
(vA-vA′)选取向左为正方向(因为已知矢量中向左的较多,这是选正方向的原则),vA="-1" m/s,vB="5" m/s,vA′="7" m/s,代入上式,得碰撞后B球的速度为:
vB′="5" m/s+
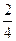 (-1-7) m/s="1" m/s
(-1-7) m/s="1" m/s即碰撞后B球速度大小为1 m/s,方向向左.

练习册系列答案
相关题目
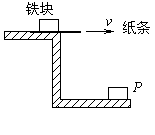
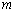 的物体以初速度
的物体以初速度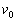 开始做平抛运动,经过时间
开始做平抛运动,经过时间 ,下降的高度为
,下降的高度为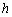 ,速度变为
,速度变为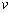 ,则这段时间内物体动量变化大小为( )
,则这段时间内物体动量变化大小为( )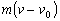
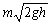
 器,其他条件不变,如题25图所示.求金属棒从开始运动到达稳定状态时电容器的带电量和电容器所储存的能量(不计电路向外辐射的能量).
器,其他条件不变,如题25图所示.求金属棒从开始运动到达稳定状态时电容器的带电量和电容器所储存的能量(不计电路向外辐射的能量).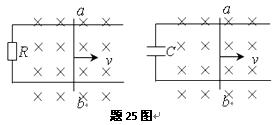
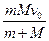
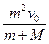

 m高处自由下落,与地面碰撞后,上升的最大高度为3.2 m,设球与地面作用时间为0.2 s,求小球对
m高处自由下落,与地面碰撞后,上升的最大高度为3.2 m,设球与地面作用时间为0.2 s,求小球对 地面的平均作用力。(g =" 10" m/s2,不计空气阻力.)[
地面的平均作用力。(g =" 10" m/s2,不计空气阻力.)[