题目内容
1. 蹦极模型简化如图甲所示,蹦极比赛中,质量60kg的运动员系在橡皮绳上,橡皮绳另一端固定在O点,运动员从O点由静止下落,下落过程中运动员的速度与下落距离间的关系如图乙所示,橡皮绳的自然长度为12m,且始终在弹性限度内,弹力大小遵循胡克定律,不计橡皮绳的质量及空气阻力,重力加速度g=10m/s2,则( )
蹦极模型简化如图甲所示,蹦极比赛中,质量60kg的运动员系在橡皮绳上,橡皮绳另一端固定在O点,运动员从O点由静止下落,下落过程中运动员的速度与下落距离间的关系如图乙所示,橡皮绳的自然长度为12m,且始终在弹性限度内,弹力大小遵循胡克定律,不计橡皮绳的质量及空气阻力,重力加速度g=10m/s2,则( )| A. | 在下落过程中运动员的机械能守恒 | |
| B. | 运动员下落过程中的最大加速度大小约为20m/s2 | |
| C. | 当橡皮绳上的拉力为1275N时,物体的速度大小约为15m/s | |
| D. | 运动员下落过程中橡皮绳的弹性势能最大值约为1×104J |
分析 根据运动学知识得速度最大时a=0,由牛顿第二定律得此时重力等于弹簧弹力,解得劲度系数,有图象得到各个状态时的伸长量,求得对应的力,根据牛顿第二定律和机械能守恒定律求解相应问题.
解答 解:A、下降过程中只有重力和弹力做功,运动员和橡皮绳的机械能守恒,减少的重力势能转化为橡皮绳的弹性势能,根据机械能守恒定律得:
最大弹性势能Ep=mgh=60×10×36J=2.16×104J,故AD错误;
B、根据牛顿第二定律得:F-mg=ma,即:1800-60×10=60a,解得:a=20m/s2,故B正确.
C、当橡皮绳上的拉力为1275 N时,由F=k△x3,解得橡皮绳的伸长量△x3=16 m,运动员下落的距离x=28 m,由图乙可知,对应的速度大小约为15 m/s,故C正确.
故选:BC
点评 本题是胡克定律与能量相结合的题目,根据运动图象确定重力和弹力关系,解得弹簧的劲度系数是解题的关键.

练习册系列答案
相关题目
9.下列所述的实例中(均不计空气阻力),机械能守恒的是( )
| A. | 小石块被竖直向上抛出后在空中运动的过程 | |
| B. | 木箱沿粗糙斜面匀速下滑的过程 | |
| C. | 人乘电梯匀速上升的过程 | |
| D. | 子弹射穿木块的过程 |
9.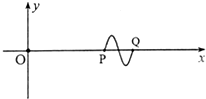 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )| A. | 第一列波的起振方向向上 | |
| B. | 第一列波的传播周期为0.1s | |
| C. | 两列波的传播速度相同 | |
| D. | 第二列波的传播周期为0.8s | |
| E. | 质点P在这1.9s内通过的路程为2.0m |
16.一个物体沿直线运动,描绘出物体的$\frac{x}{t}$-t图象如图所示,则下列判断正确的是( )


| A. | 物体做匀速直线运动 | B. | 物体做变加速直线运动 | ||
| C. | 物体的初速度大小为-1m/s | D. | 物体的加速度大小为1m/s2 |
6.若未来地球自转速度在逐渐增大,地球的质量与半径不变,则未来发射的地球同步卫星与现在的相比( )
| A. | 离地面高度变大 | B. | 角速度变小 | C. | 向心加速度变大 | D. | 线速度变小 |
13. 如图所示,虚线MN上方存在垂直纸面向里的匀强磁场,MN下方存在竖直向下的匀强磁场,两处磁场磁感应强度大小均为B0.足够长的不等间距金属导轨竖直放置,导轨电阻不计.两根金属棒通过棒两端的套环水平地套在金属导轨上,其中光滑金属棒AB质量为m,长为L,电阻为R;金属棒CD质量为2m、长为2L、电阻为2R,与导轨之间的动摩擦因数为μ.若AB棒在外力F的作用下向上做匀速运动,CD棒向下做匀速运动,下列说法正确的是( )
如图所示,虚线MN上方存在垂直纸面向里的匀强磁场,MN下方存在竖直向下的匀强磁场,两处磁场磁感应强度大小均为B0.足够长的不等间距金属导轨竖直放置,导轨电阻不计.两根金属棒通过棒两端的套环水平地套在金属导轨上,其中光滑金属棒AB质量为m,长为L,电阻为R;金属棒CD质量为2m、长为2L、电阻为2R,与导轨之间的动摩擦因数为μ.若AB棒在外力F的作用下向上做匀速运动,CD棒向下做匀速运动,下列说法正确的是( )
 如图所示,虚线MN上方存在垂直纸面向里的匀强磁场,MN下方存在竖直向下的匀强磁场,两处磁场磁感应强度大小均为B0.足够长的不等间距金属导轨竖直放置,导轨电阻不计.两根金属棒通过棒两端的套环水平地套在金属导轨上,其中光滑金属棒AB质量为m,长为L,电阻为R;金属棒CD质量为2m、长为2L、电阻为2R,与导轨之间的动摩擦因数为μ.若AB棒在外力F的作用下向上做匀速运动,CD棒向下做匀速运动,下列说法正确的是( )
如图所示,虚线MN上方存在垂直纸面向里的匀强磁场,MN下方存在竖直向下的匀强磁场,两处磁场磁感应强度大小均为B0.足够长的不等间距金属导轨竖直放置,导轨电阻不计.两根金属棒通过棒两端的套环水平地套在金属导轨上,其中光滑金属棒AB质量为m,长为L,电阻为R;金属棒CD质量为2m、长为2L、电阻为2R,与导轨之间的动摩擦因数为μ.若AB棒在外力F的作用下向上做匀速运动,CD棒向下做匀速运动,下列说法正确的是( )| A. | AB棒中电流方向从A到B | |
| B. | AB棒匀速运动的速度$\frac{3mgR}{μ{B}_{0}^{2}{L}^{2}}$ | |
| C. | 时间t内CD棒上的焦耳热为$\frac{3{m}^{2}{g}^{2}Rt}{{μ}^{2}{B}_{0}^{2}{L}^{2}}$ | |
| D. | AB杆所受拉力F=mg+$\frac{1}{μ}$mg |
11. 甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )
甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )
 甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )
甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )| A. | 运动的加速度之比为5:1 | |
| B. | 相遇前的平均速度相等 | |
| C. | 到达同一位置前相距最远距离为180m | |
| D. | 到达同一位置前相距最远距离为400m |
 有一轻质杆,长l=0.5m,一段固定一质量m=0.5kg的小球,轻杆绕另一端在竖直面内做圆周运动.
有一轻质杆,长l=0.5m,一段固定一质量m=0.5kg的小球,轻杆绕另一端在竖直面内做圆周运动.