题目内容
11.表是某金属线材的试验数据| 长度 | 拉力 伸长 截面积 | 250N | 500N | 750N | 1000N |
| 1m | 0.05cm2 | 0.04cm | 0.08cm | 0.12cm | 0.16cm |
| 2m | 0.05cm2 | 0.08cm | 0.16cm | 0.24cm | 0.32cm |
| 1m | 0.10cm2 | 0.02cm | 0.04cm | 0.06cm | 0.08cm |
(1)本实验采用哪种实验方法D
A.等效替代法 B.理想化方法 C.类比法 D.控制变量法
(2 )总结上述分析,该金属线材伸长量X随拉力F、长度L、横截面积S的变化而变化,其表达式X=x=k $\frac{FL}{S}$.
(3)现有一根用上述材料所制成的金属杆,长为4m,横截面积为0.8cm2,设计要求它受到拉力后伸长不超过原长的$\frac{1}{1000}$,则受到的最大拉力为1×104N.
分析 (1)由题可知伸长量x与样品的长度、横截面积、所受拉力都有关系,涉及的变量较多,因此采用“控制变量法”来确定它们之间的正、反比关系,然后将各种情况进行汇总,再运用比值定义法初步确定这几个量之间的数量关系,然后根据所得公式来判断样品能承受的最大拉力,以及与什么因素有关.
(2)一个物理量与几个变量之间都有关系时,常常采用控制变量法研究;
(3)根据(1)表达式,求最大拉力.
解答 解:(1)由表格知:
1、当受到的拉力F、横截面积S一定时,伸长量x与样品长度L成正比,①
2、当受到的拉力F、样品长度L一定时,伸长量x与横截面积S成反比,②
3、当样品长度L、横截面积S一定时,伸长量x与受到的拉力F成正比,③
由①②③三个结论,可以归纳出,x与L、S、F之间存在一定量的比例关系,设这个比值为k,那么有:$x=k\frac{FL}{S}$(其中k为比例系数)
由上知,线材伸长x与材料的长度L、材料的横截面积S及拉力F都有关系,可采用控制变量法,故选D
(3)根据图表提供数据代入解得:k=$\frac{2}{25}$×10-2m2/N.
由题意知:待测金属杆M承受最大拉力时,其伸长量为原来的$\frac{1}{1000}$,即4×10-3m;
此时 S=0.8cm2=8×10-5m2,L=4m;代入上面的公式①解得:F=1×104N.
故答案为:
(1)D
(2)$x=k\frac{FL}{S}$(其中k为比例系数)
(3)1×104
点评 本题中共涉及4个变量,在解题过程中,综合应用了控制变量法、归纳法、比值定义法来进行分析、解答,对同学的综合素质要求很高,是一道考查能力的好题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
1. 如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.现使线框保持图中所示位置,磁感应强度大小随时间线性变化.为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率$\frac{△B}{△t}$的大小应为( )
如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.现使线框保持图中所示位置,磁感应强度大小随时间线性变化.为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率$\frac{△B}{△t}$的大小应为( )
 如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.现使线框保持图中所示位置,磁感应强度大小随时间线性变化.为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率$\frac{△B}{△t}$的大小应为( )
如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.现使线框保持图中所示位置,磁感应强度大小随时间线性变化.为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率$\frac{△B}{△t}$的大小应为( )| A. | $\frac{ω{B}_{0}}{π}$ | B. | $\frac{2ω{B}_{0}}{π}$ | C. | $\frac{4ω{B}_{0}}{π}$ | D. | $\frac{ω{B}_{0}}{2π}$ |
6. 如图所示,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上.一电阻为r,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形.棒与导轨间光滑、棒左侧有两个固定于水平面的光滑立柱.导轨bc段电阻为R,长为L,其他部分电阻不计.以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向右,磁感应强度大小均为B.在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a.则( )
如图所示,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上.一电阻为r,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形.棒与导轨间光滑、棒左侧有两个固定于水平面的光滑立柱.导轨bc段电阻为R,长为L,其他部分电阻不计.以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向右,磁感应强度大小均为B.在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a.则( )
 如图所示,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上.一电阻为r,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形.棒与导轨间光滑、棒左侧有两个固定于水平面的光滑立柱.导轨bc段电阻为R,长为L,其他部分电阻不计.以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向右,磁感应强度大小均为B.在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a.则( )
如图所示,质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上.一电阻为r,质量为m的导体棒PQ放置在导轨上,始终与导轨接触良好,PQbc构成矩形.棒与导轨间光滑、棒左侧有两个固定于水平面的光滑立柱.导轨bc段电阻为R,长为L,其他部分电阻不计.以ef为界,其左侧匀强磁场方向竖直向上,右侧匀强磁场水平向右,磁感应强度大小均为B.在t=0时,一水平向左的拉力F垂直作用在导轨的bc边上,使导轨由静止开始做匀加速直线运动,加速度为a.则( )| A. | F与t成反比 | |
| B. | F与t2成正比 | |
| C. | 当t达到一定值时,QP刚好对轨道无压力 | |
| D. | 若F=0,PQbc静止,ef左侧磁场均匀减小,当$\frac{△B}{△t}$达到一定值时,QP刚好对轨道无压力 |
9.质量为m的小球在竖直平面内的圆形轨道的内侧运动,经过最高而不脱离轨道的临界速度值是v,当小球以2v的速度经过最高点时,对轨道的压力值是( )
| A. | mg | B. | 2mg | C. | 3mg | D. | 4mg |
10. 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )
 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )| A. | (mg-f)(H-L+x) | B. | mg(H-L+x)-f(H-L) | C. | mgH-f(H-L) | D. | mg(L-x)+f(H-L+x) |
 “抛石机”是古代战争中常用的一种设备,它实际上是一个费力杠杆.如图所示,某中学“研学小组”用自制的抛石机演练抛石过程.所用抛石机长臂的长度L=4.8m,质量m=5kg的石块装在长臂末端的口袋中.开始时长臂与水平面间的夹角为α=30°,对短臂施力,使石块经较长路径获得较大的速度,当长臂转到竖直位置时立即停止转动,石块被水平抛出,石块落地位置与抛出点间的水平距离s=19.2m.不计空气的阻力,当地重力加速度取g=10m/s2.求:
“抛石机”是古代战争中常用的一种设备,它实际上是一个费力杠杆.如图所示,某中学“研学小组”用自制的抛石机演练抛石过程.所用抛石机长臂的长度L=4.8m,质量m=5kg的石块装在长臂末端的口袋中.开始时长臂与水平面间的夹角为α=30°,对短臂施力,使石块经较长路径获得较大的速度,当长臂转到竖直位置时立即停止转动,石块被水平抛出,石块落地位置与抛出点间的水平距离s=19.2m.不计空气的阻力,当地重力加速度取g=10m/s2.求: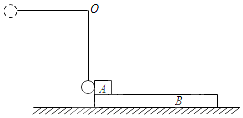 质量为M=6kg的木板B静止于光滑水平面上,物块A质量为6kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.2,为使A、B达到共同速度前A不滑离木板,木板至少多长?
质量为M=6kg的木板B静止于光滑水平面上,物块A质量为6kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.2,为使A、B达到共同速度前A不滑离木板,木板至少多长?