题目内容
19.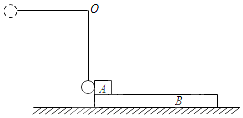 质量为M=6kg的木板B静止于光滑水平面上,物块A质量为6kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.2,为使A、B达到共同速度前A不滑离木板,木板至少多长?
质量为M=6kg的木板B静止于光滑水平面上,物块A质量为6kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.2,为使A、B达到共同速度前A不滑离木板,木板至少多长?
分析 对小球下落过程应用机械能守恒定律求出小球到达A时的速度,再由机械能守恒定律求得球反弹上升的初速度即球与A碰后的速度,再根据动量守恒定律求得球与A碰撞后A的速度;A没有滑离B,A、B共同运动,由动量守恒定律列方程求二者共同的速度,由摩擦力做功的特点即可求得木板的长度.
解答 解:小球下摆过程机械能守恒,由机械能守恒定律得:
mgL=$\frac{1}{2}$mv12,
代入数据解得:v1=4m/s,
小球反弹后上升过程,机械能守恒,由机械能守恒定律得:
mgh=$\frac{1}{2}$mv1′2,
代入数据解得:v1′=2m/s,
球与A碰撞过程中,系统动量守恒,以球的初速度方向为正方向,由动量守恒定律得:
mv1=-m1v1′+mAvA,
代入数据解得:vA=1m/s,
物块A与木板B相互作用过程,系统动量守恒,以A的速度方向为正方向,由动量守恒定律得:
mAvA=(mA+M)v,
代入数据解得:v=0.5m/s;
由能量守恒定律得:μmAgx=$\frac{1}{2}$mAvA2-$\frac{1}{2}$(mA+M)v2,
代入数据解得:x=0.125m;
答:为使A、B达到共同速度前A不滑离木板,木板至少长0.125m.
点评 本题关键是根据动量守恒定律、动量定理、能量守恒列式求解,应用动量守恒解题时要注意选取合适的系统作为研究对象,判断是否符合动量守恒的条件,注意选取正方向.

练习册系列答案
相关题目
10.一个人站在阳台上,以相同的速率分别把三个球竖直向下、竖直向上、水平抛出.不计空气阻力.则( )
| A. | 平抛球在空中运动时间最长 | B. | 上抛球在空中运动时间最长 | ||
| C. | 三球落地时,上抛球速度最小 | D. | 三球落地时,下抛球速度最小 |
7. 如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左、右两侧传播,波速均为v.当波源起振后经过时间△t1,A点起振,再经过时间△t2,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )
如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左、右两侧传播,波速均为v.当波源起振后经过时间△t1,A点起振,再经过时间△t2,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )
 如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左、右两侧传播,波速均为v.当波源起振后经过时间△t1,A点起振,再经过时间△t2,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )
如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左、右两侧传播,波速均为v.当波源起振后经过时间△t1,A点起振,再经过时间△t2,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )| A. | A、B两点的起振方向相反 | |
| B. | 波源周期的最大值为△t2 | |
| C. | 该列横波的波长为$\frac{2v△{t}_{2}}{2n+1}$(n=0,1,2,…) | |
| D. | A、B两点之间的距离一定为半波长的奇数倍 |
14.下列说法中正确的是( )
| A. | 只要知道气体的摩尔体积和阿伏伽德罗常数,就可以算出气体分子的体积 | |
| B. | 液晶像液体一样具有流动性,而其光学性质和某些晶体相似 | |
| C. | 当人们感到潮湿时,空气的相对湿度一定较大 | |
| D. | 用打气筒的活塞压缩气体很费力,说明分子间有斥力 | |
| E. | 物体的温度越高,分子热运动越剧烈,分子的平均动能就越大 |
4.下列说法正确的是 ( )
| A. | 光子像其他粒子一样,不仅具有能量,也具有动量 | |
| B. | 波尔认为,原子中电子轨道是量子化的,能量也是量子化的 | |
| C. | β射线是原子核外电子高速运动形成的 | |
| D. | 原子核的质量大于组成它的核子的质量之和,这个现象叫质量亏损 | |
| E. | 根据波尔理论可知,氢原子辐射出一个光子后,氢原子的电势能减少,动能增加 |
11.表是某金属线材的试验数据
请你利用上述实验数据回答下列问题:
(1)本实验采用哪种实验方法D
A.等效替代法 B.理想化方法 C.类比法 D.控制变量法
(2 )总结上述分析,该金属线材伸长量X随拉力F、长度L、横截面积S的变化而变化,其表达式X=x=k $\frac{FL}{S}$.
(3)现有一根用上述材料所制成的金属杆,长为4m,横截面积为0.8cm2,设计要求它受到拉力后伸长不超过原长的$\frac{1}{1000}$,则受到的最大拉力为1×104N.
| 长度 | 拉力 伸长 截面积 | 250N | 500N | 750N | 1000N |
| 1m | 0.05cm2 | 0.04cm | 0.08cm | 0.12cm | 0.16cm |
| 2m | 0.05cm2 | 0.08cm | 0.16cm | 0.24cm | 0.32cm |
| 1m | 0.10cm2 | 0.02cm | 0.04cm | 0.06cm | 0.08cm |
(1)本实验采用哪种实验方法D
A.等效替代法 B.理想化方法 C.类比法 D.控制变量法
(2 )总结上述分析,该金属线材伸长量X随拉力F、长度L、横截面积S的变化而变化,其表达式X=x=k $\frac{FL}{S}$.
(3)现有一根用上述材料所制成的金属杆,长为4m,横截面积为0.8cm2,设计要求它受到拉力后伸长不超过原长的$\frac{1}{1000}$,则受到的最大拉力为1×104N.
18.跳高时要铺上厚厚的垫子,这是为了( )
| A. | 减少运动员受到的冲量? | B. | 减少运动员受到的冲力? | ||
| C. | 减少运动员的动量的变化? | D. | 减小运动员的惯性? |
 如图所示,在水平转盘上,距转动轴20cm处有一个质量为20g的小木块,当转盘的转动周期为2s时,木块与转盘之间没有相对滑动,问木块受几个力?每个力是多大?方向怎样?
如图所示,在水平转盘上,距转动轴20cm处有一个质量为20g的小木块,当转盘的转动周期为2s时,木块与转盘之间没有相对滑动,问木块受几个力?每个力是多大?方向怎样?