题目内容
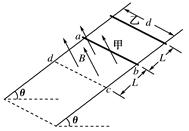
在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=37°的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行.劲度系数k=5 N/m的轻弹簧一端固定在O点,一端用另一轻绳穿过固定的光滑小环D与A相连,弹簧处于原长,轻绳恰好拉直,DM垂直于斜面.水平面处于场强E=5×104 N/C、方向水平向右的匀强电场中.已知A、B的质量分别为mA=0.1 kg和mB=0.2 kg,B所带电荷量q=+4×10-6 C.设两物体均视为质点,不计滑轮质量和摩擦,绳不可伸长,弹簧始终在弹性限度内,B电荷量不变.取g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
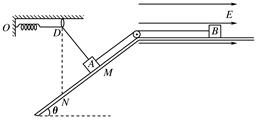
(1)求B所受静摩擦力的大小;
(2)现对A施加沿斜面向下的拉力F,使A以加速度a=0.6 m/s2开始做匀加速直线运动.A从M到N的过程中,B的电势能增加了ΔEp=0.06 J.已知DN沿竖直方向,B与水平面间的动摩擦因数μ=0.4.求A到达N点时拉力F的瞬时功率.

(1)求B所受静摩擦力的大小;
(2)现对A施加沿斜面向下的拉力F,使A以加速度a=0.6 m/s2开始做匀加速直线运动.A从M到N的过程中,B的电势能增加了ΔEp=0.06 J.已知DN沿竖直方向,B与水平面间的动摩擦因数μ=0.4.求A到达N点时拉力F的瞬时功率.
(1)0.4 N (2) 0.258 W
A、B处于静止状态时,对于A、B根据共点力的平衡条件解决问题;当A、B做匀加速直线运动时,根据运动学公式、牛顿第二定律和功能关系解决问题.
(1)F作用之前,A、B处于静止状态.设B所受静摩擦力大小为Ff0,A、B间绳中张力为FT0,有
对A:FT0=mAgsin θ ①
对B:FT0=qE+Ff0 ②
联立①②式,代入数据解得Ff0=0.4 N.③
(2)物体A从M点到N点的过程中,A、B两物体的位移均为x,A、B间绳子张力为FT,有
qEx=ΔEp ④
FT-μmBg-qE=mBa ⑤
设A在N点时速度为v,受弹簧拉力为F弹,弹簧的伸长量为Δx,有
v2=2ax ⑥
F弹=k·Δx ⑦
F+mAgsin θ-F弹sin θ-FT=mAa ⑧
由几何关系知Δx=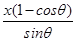 ⑨
⑨
设拉力F的瞬时功率为P,有P=Fv⑩
联立④~⑩式,代入数据解得
P=0.528 W.
(1)F作用之前,A、B处于静止状态.设B所受静摩擦力大小为Ff0,A、B间绳中张力为FT0,有
对A:FT0=mAgsin θ ①
对B:FT0=qE+Ff0 ②
联立①②式,代入数据解得Ff0=0.4 N.③
(2)物体A从M点到N点的过程中,A、B两物体的位移均为x,A、B间绳子张力为FT,有
qEx=ΔEp ④
FT-μmBg-qE=mBa ⑤
设A在N点时速度为v,受弹簧拉力为F弹,弹簧的伸长量为Δx,有
v2=2ax ⑥
F弹=k·Δx ⑦
F+mAgsin θ-F弹sin θ-FT=mAa ⑧
由几何关系知Δx=
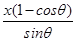 ⑨
⑨设拉力F的瞬时功率为P,有P=Fv⑩
联立④~⑩式,代入数据解得
P=0.528 W.

练习册系列答案
相关题目

 )
)