题目内容
5.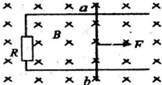 如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直导轨所在平面,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨电阻不计.现将金属棒沿导轨由静止向右拉,若保持拉力F值定,经时间t1后速度为v,加速度为a1,最终以速度2v做匀速运动:若保持拉力的功率恒定,棒由静止经时间t2后速度为v,加速度为a2,最终也以速度2v做匀速运动,则( )
如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直导轨所在平面,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨电阻不计.现将金属棒沿导轨由静止向右拉,若保持拉力F值定,经时间t1后速度为v,加速度为a1,最终以速度2v做匀速运动:若保持拉力的功率恒定,棒由静止经时间t2后速度为v,加速度为a2,最终也以速度2v做匀速运动,则( )| A. | t2=t1 | B. | t1>t2 | C. | a2=2a1 | D. | a2=3a1 |
分析 分析清楚两种情况下的运动形式区别,然后根据牛顿第二定律和运动学规律求解,注意两种情况下导体棒最终匀速运动时所受拉力大小是相同的.
解答 解:C、D由于两种情况下,最终棒都以速度2v匀速运动,此时拉力与安培力大小相等,则有:
F=F安=BIL=BL$•\frac{BL•2v}{R}$=$\frac{2{B}^{2}{L}^{2}v}{R}$…①
当拉力恒定,速度为v,加速度为a1时,根据牛顿第二定律有:F-$\frac{{B}^{2}{L}^{2}v}{R}$=ma1…②
由①②解得:a1=$\frac{{B}^{2}{L}^{2}v}{Rm}$.
若保持拉力的功率恒定,速度为2v时,拉力为F,则有:P=F•2v,
又F=F安=$\frac{2{B}^{2}{L}^{2}v}{R}$
所以P=$\frac{4{B}^{2}{L}^{2}{v}^{2}}{R}$
则当速度为v时,拉力大小为:F1=$\frac{P}{v}$=$\frac{4{B}^{2}{L}^{2}v}{R}$;
根据牛顿第二定律,得:
F1-$\frac{{B}^{2}{L}^{2}v}{R}$=ma2,解得:a2=$\frac{3{B}^{2}{L}^{2}v}{Rm}$,所以有a2=3a1,故C错误,D正确;
A、B当拉力的功率恒定时,随着速度增大,拉力逐渐减小,最后匀速运动时拉力最小,且最小值和第一种情况下拉力相等,因此最后都达到速度2V时,t1>t2,故A错误,B正确.
故选:BD
点评 本题可以和机车启动的两种方式进行类比解答,只不过机车启动时阻力不变,而该题中阻力为安培力,是不断变化的.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
20.关于分子动理论和物体的内能,下列说法正确的是( )
| A. | “油膜法”估测分子大小实验中,可将纯油酸直接滴入浅盘的水面上 | |
| B. | 温度越高,液体中悬浮微粒的布朗运动就越明显 | |
| C. | 分子间的引力和斥力都随着分子间距离的增大而减小 | |
| D. | 分子间的引力和斥力相等时,分子势能一定为零 | |
| E. | 物体温度降低时,其分子热运动的平均动能一定减小 |
10.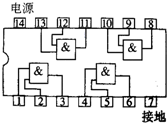 如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )
如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )
 如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )
如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )| A. | 1 0 | B. | 0 1 | C. | 1 1 | D. | 0 0 |
14.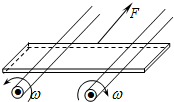 如图所示,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两圆柱等距,其中圆柱的半径r=2cm,木板质量m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以角速度ω绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力F于木板上,使其以速度v=0.6m/s沿圆柱表面作匀速运动.取g=10m/s2.下列说法中正确的是( )
如图所示,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两圆柱等距,其中圆柱的半径r=2cm,木板质量m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以角速度ω绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力F于木板上,使其以速度v=0.6m/s沿圆柱表面作匀速运动.取g=10m/s2.下列说法中正确的是( )
 如图所示,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两圆柱等距,其中圆柱的半径r=2cm,木板质量m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以角速度ω绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力F于木板上,使其以速度v=0.6m/s沿圆柱表面作匀速运动.取g=10m/s2.下列说法中正确的是( )
如图所示,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两圆柱等距,其中圆柱的半径r=2cm,木板质量m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以角速度ω绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力F于木板上,使其以速度v=0.6m/s沿圆柱表面作匀速运动.取g=10m/s2.下列说法中正确的是( )| A. | 若ω=0,则水平拉力F=20N | |
| B. | 若ω=40rad/s,则水平拉力F=6N | |
| C. | 若ω=40rad/s,木板移动距离x=0.5m,则拉力所做的功为4J | |
| D. | 不论ω为多大,所需水平拉力恒为10N |
15.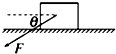 如图所示,质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,木块受到的滑动摩擦力为下列各值中的哪个( )
如图所示,质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,木块受到的滑动摩擦力为下列各值中的哪个( )
 如图所示,质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,木块受到的滑动摩擦力为下列各值中的哪个( )
如图所示,质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,木块受到的滑动摩擦力为下列各值中的哪个( )| A. | μmg | B. | μ(mg+Fsinθ) | C. | μ(mg+Fcosθ) | D. | Fcosθ |
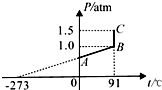 某同学研究一定质量理想气体的状态变化,得出如下的P-t图象.已知在状态B时气体的体积VB=3L,求
某同学研究一定质量理想气体的状态变化,得出如下的P-t图象.已知在状态B时气体的体积VB=3L,求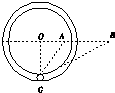 如图所示,在竖直面上固定着一根光滑绝缘的圆形空心管,其圆心在O点.过O点的一条水平直径及其延长线上的A、B两点固定着两个电荷.其中固定于A点的为正电荷,所带的电荷量为Q;固定于B点的是未知电荷.在它们形成的电场中,有一个可视为质点的质量为m、带电荷量为q的小球正在空心管中做圆周运动,若已知小球以某一速度通过最低点C处时,小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度,A、B间的距离为L,∠ABC=∠ACB=30°.CO⊥OB,静电力常量为k.
如图所示,在竖直面上固定着一根光滑绝缘的圆形空心管,其圆心在O点.过O点的一条水平直径及其延长线上的A、B两点固定着两个电荷.其中固定于A点的为正电荷,所带的电荷量为Q;固定于B点的是未知电荷.在它们形成的电场中,有一个可视为质点的质量为m、带电荷量为q的小球正在空心管中做圆周运动,若已知小球以某一速度通过最低点C处时,小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度,A、B间的距离为L,∠ABC=∠ACB=30°.CO⊥OB,静电力常量为k.