题目内容
17. 如图所示,在竖直面上固定着一根光滑绝缘的圆形空心管,其圆心在O点.过O点的一条水平直径及其延长线上的A、B两点固定着两个电荷.其中固定于A点的为正电荷,所带的电荷量为Q;固定于B点的是未知电荷.在它们形成的电场中,有一个可视为质点的质量为m、带电荷量为q的小球正在空心管中做圆周运动,若已知小球以某一速度通过最低点C处时,小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度,A、B间的距离为L,∠ABC=∠ACB=30°.CO⊥OB,静电力常量为k.
如图所示,在竖直面上固定着一根光滑绝缘的圆形空心管,其圆心在O点.过O点的一条水平直径及其延长线上的A、B两点固定着两个电荷.其中固定于A点的为正电荷,所带的电荷量为Q;固定于B点的是未知电荷.在它们形成的电场中,有一个可视为质点的质量为m、带电荷量为q的小球正在空心管中做圆周运动,若已知小球以某一速度通过最低点C处时,小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度,A、B间的距离为L,∠ABC=∠ACB=30°.CO⊥OB,静电力常量为k.(1)确定小球和固定在B点的电荷的带电性质.
(2)求固定在B点的电荷所带的电荷量.
(3)求小球运动到最高点处,空心管对小球作用力.
分析 (1)小球做圆周运动,必须有向心力,根据小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度可知,小球在C点的合力方向一定沿CO且指向O点,作出力图,即可判断出小球带负电,B带负电.
(2)根据小球在C点无切向加速度,切线方向力平衡,根据库仑定律列式求得B的电荷量.
(3)对C点受力分析根据牛顿运动定律和动能定理进行解答.
解答 解:(1)由小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,可知小球在C点的合力方向一定沿CO且指向O点,所以A处电荷对小球吸引,B处电荷对小球排斥,因为A处电荷为正,所以小球带负电,B带负电.
(2)因为∠ABC=∠ACB=30°,CO⊥OB,由几何关系得:BC=2ABcos30°=$\sqrt{3}$L
由于无切向加速度,小球沿切线方向的合力为零,则有:
k$\frac{qQ}{{L}^{2}}$cos60°=k$\frac{q{Q}_{B}}{(\sqrt{3}L)^{2}}$cos30°,
解得:QB=$\sqrt{3}$Q;
(3)设小球在最低点C处的速度为vC,
则:F-mg=m$\frac{{v}_{C}^{2}}{R}$,
小球从C点运动到最高点的过程中,电势能不变,故由动能定理知: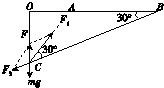
2mgR=$\frac{1}{2}$mvC2-$\frac{1}{2}$mv2,
小球在最高点受到A、B电荷的作用力合为F,方向竖直向下
即:F+mg-F管=m$\frac{{v}^{2}}{R}$,
解得:F管=6mg,故空心管对小球的作用力大小为6mg,方向竖直向上.
答:(1)小球带负电,B处电荷带负电;
(2)固定在B点的电荷所带的电荷量为$\sqrt{3}$Q.
(3)小球运动到最高点处,空心管对小球作用力的大小为6mg,方向竖直向上.
点评 本题的突破口是“小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度”,分析小球的受力情况,确定出向心力,判断小球与B的电性.

 如图所示,有效值为U的正弦式交流电源通过理想变压器给纯电阻R供电,在变压器原线圈上串有纯电阻r,原副线圈匝数之比n1:n2=1:2,当R取下列何值时,R消耗的功率最大?
如图所示,有效值为U的正弦式交流电源通过理想变压器给纯电阻R供电,在变压器原线圈上串有纯电阻r,原副线圈匝数之比n1:n2=1:2,当R取下列何值时,R消耗的功率最大?| A. | r | B. | 2r | C. | 4r | D. | 8r |
 如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直导轨所在平面,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨电阻不计.现将金属棒沿导轨由静止向右拉,若保持拉力F值定,经时间t1后速度为v,加速度为a1,最终以速度2v做匀速运动:若保持拉力的功率恒定,棒由静止经时间t2后速度为v,加速度为a2,最终也以速度2v做匀速运动,则( )
如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直导轨所在平面,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨电阻不计.现将金属棒沿导轨由静止向右拉,若保持拉力F值定,经时间t1后速度为v,加速度为a1,最终以速度2v做匀速运动:若保持拉力的功率恒定,棒由静止经时间t2后速度为v,加速度为a2,最终也以速度2v做匀速运动,则( )| A. | t2=t1 | B. | t1>t2 | C. | a2=2a1 | D. | a2=3a1 |
| A. | 一个电源的电动势的大小只由电源本身决定 | |
| B. | 因电动势的单位和电势差相同,所以电动势实质上就是电势差 | |
| C. | 一个电动势为1.5V的电源接入电路时,若有1C的电荷量通过电路,电源就有1.5J的电能转变成化学能 | |
| D. | 电压表接到电源两极时,测得的就是电动势 |
| A. | 7 | B. | 8 | C. | 64 | D. | 63 |
| A. | 有多余的电子 | B. | 有多余的质子 | C. | 有多余的原子 | D. | 缺少电子 |

| A. | 氢原子从高能级向低能级跃迁时会吸收能量 | |
| B. | 氢原子从n=4的激发态向n=3的激发态跃迁时不可能辐射出可见光 | |
| C. | 处于n=4的激发态的氢原子从n=4的激发态向n=1的基态跃迁时,辐射出的光子频率最大 | |
| D. | 要使处于基态的氢原子变成氢离子至少要吸收13.6eV的能量 | |
| E. | 大量氢原子从n=4的激发态向n=1的基态跃迁时,能发出三种频率的光子 |
| A. | 传说中的“天上一日,人间一年”与狭义相对论中“时间的相对性”是相悖的 | |
| B. | 相对论时空观认为时间和空间的量度是与物体的运动有关的 | |
| C. | 振荡电路发射电磁波的条件是要有足够高的振荡频率和足够大的电流 | |
| D. | 红外线是一种频率比紫外线还高的电磁波 |
 如图为利用小球做自由落体运动验证机械能守恒的实验装置图,O点是释放小球的初始位置,光电门位于其正下方.已知小球的直径为d.
如图为利用小球做自由落体运动验证机械能守恒的实验装置图,O点是释放小球的初始位置,光电门位于其正下方.已知小球的直径为d.