题目内容
16.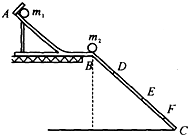 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不等的小球,按下述步骤做了如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不等的小球,按下述步骤做了如下实验:①用天平测出两个小球的质量分别为m1和m2,且m1>m2.
②按照如图所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平.将一斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2放在斜槽前端边缘处,让小球m1从斜槽顶端A处滚下,使它们发生碰撞,记下小球m1和小球m2在斜面上的落点位置.
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离.图中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD、LE、LF. 根据该同学的实验,回答下列问题:
(1)小球m1与m2发生碰撞后,m1的落点是图中的D点,m2的落点是图中的F点.
(2)用测得的物理量来表示,只要满足关系式${m_1}\sqrt{L_E}={m_1}\sqrt{L_D}+{m_2}\sqrt{L_F}$,则说明碰撞中动量是守恒的.
(3)用测得的物理量来表示,只要再满足关系式m1LE=m1LD+m2LF,则说明两小球的碰撞是弹性碰撞.
分析 (1)小球m1和小球m2相撞后,小球m2的速度增大,小球m1的速度减小,都做平抛运动,由平抛运动规律不难判断出;
(2)设斜面BC与水平面的倾角为α,由平抛运动规律求出碰撞前后小球m1和小球m2的速度,表示出动量的表达式即可求解;
(3)若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.
解答 解:(1)小球m1和小球m2相撞后,小球m2的速度增大,小球m1的速度减小,都做平抛运动,所以碰撞后m1球的落地点是D点,m2球的落地点是F点;
(2)碰撞前,小于m1落在图中的E点,设其水平初速度为v1.小球m1和m2发生碰撞后,m1的落点在图中的D点,设其水平初速度为v1′,m2的落点是图中的F点,设其水平初速度为v2. 设斜面BC与水平面的倾角为α,
由平抛运动规律得:${L}_{D}sinα=\frac{1}{2}{gt}^{2}$,LDcosα=v′1t
解得:${v′}_{1}=\sqrt{\frac{{{gL}_{D}(cosα)}^{2}}{2sinα}}$
同理可解得:${v}_{1}=\sqrt{\frac{{{gL}_{E}(cosα)}^{2}}{2sinα}}$,${v}_{2}=\sqrt{\frac{{{gL}_{F}(cosα)}^{2}}{2sinα}}$
所以只要满足m1v1=m2v2+m1v′1即:${m}_{1}\sqrt{{L}_{E}}={m}_{1}\sqrt{{L}_{D}}+{m}_{2}\sqrt{{L}_{F}}$则说明两球碰撞过程中动量守恒;
(3)若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.则要满足关系式
$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v′12+$\frac{1}{2}$m2v2
即:m1LE=m1LD+m2LF
故答案为:(1)D;F
(2)${m_1}\sqrt{L_E}={m_1}\sqrt{L_D}+{m_2}\sqrt{L_F}$
(3)m1LE=m1LD+m2LF
点评 学会运用平抛运动的基本规律求解碰撞前后的速度,两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失.

| A. | 飞机起飞时飞机中的乘客 | |
| B. | 离开跳台后正在空中做动作的跳水运动员 | |
| C. | 正在减速下降电梯里的人 | |
| D. | 沿椭圆轨道运行的飞船中的宇航员 |
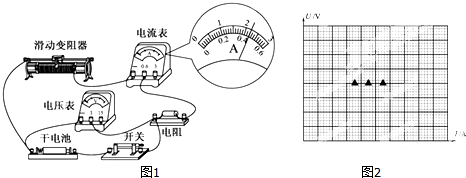
(1)图中电流表的示数为0.44A
(2)调节滑动变阻器,电压表和电流表的示数记录如下
| U/V | 1.45 | 1.36 | 1.27 | 1.16 | 1.06 |
| I/A | 0.12 | 0.20 | 0.28 | 0.36 | 0.44 |
由图线求得:电动势E=1.60V,内阻r=1.2Ω.
 如图所示,水平传送带在电机驱动下匀速运动,某时刻将一质量m=1kg的小物块以v0=1m/s的初速度从传送带左端滑上传送带,此后小物块在传送带上运动的v-t图象如图所示.重力加速度g=10m/s2,求
如图所示,水平传送带在电机驱动下匀速运动,某时刻将一质量m=1kg的小物块以v0=1m/s的初速度从传送带左端滑上传送带,此后小物块在传送带上运动的v-t图象如图所示.重力加速度g=10m/s2,求