Question

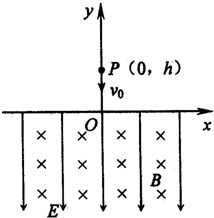如图，Oxy在竖直平面内．X轴下方有匀强电场和匀强磁场．电场强度为E、方向竖直向下．磁感应强度为B、方向垂直纸面向里．将一个带电小球从y轴上P（0，h）点以初速度v₀竖直向下抛出．小球穿过x轴后，恰好做匀速圆周运动．不计空气阻力，已知重力加速度为g．求：
（1）判断不球带正电还是带负电；
（2）小球做圆周运动的半径；
（3）小球从P点出发，到第二次经过x轴所用的时间．

Answer 1

分析：（1）小球恰好做匀速圆周运动，则重力与电场力大小相等、方向相反，据此判断小球的电性
（2）由洛伦兹力提供向心力，结合牛顿第二定律列方程得到半径
（3）小球先做匀加速直线运动，后该做圆周运动，分别求出时间便可得到总时间

解答：解：画出小球运动的轨迹示意图  

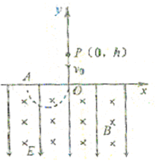
（1）小球穿过x轴后恰好做匀速圆周运动
有qE=mg  
方向竖直向上，故小球带负电
（2）设小球经过O点时的速度为v，从P到O由匀变速运动规律得：
v²=v₀²+2gh  
从O到A，根据牛顿第二定律
qvB=

mv2

r

故有：r=

E v 2 0 +2gh

gB

（3）设从P到O，小球第一次经过x轴所用时间为t₁，
则：v=v₀+gt₁ 
而v2

-v

2 0

=2gh
故t1=

v 2 0 +2gh -v0

g

设从O到A，小球第二次经过x轴，所用时间为t₂
则：t2=

T

2

=

πr

v

=

πE

gB

小球从P点出发，到第二次经过x轴所用的时间：
t=t₁+t₂=

v 2 0 +2gh -v0

g

+

πE

gB

答：（1）小球带负电
（2）小球运动半径r=

E v 2 0 +2gh

gB

（3）小球从P点出发，到第二次经过x轴所用的时间t=

v 2 0 +2gh -v0

g

+

πE

gB

点评：挖掘出小球恰好做匀速圆周运动的隐含条件为：重力与电场力大小相等、方向相反；将小球的运动划分为两个过程分别研究