题目内容
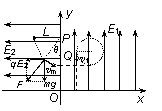
如图所示，直角坐标平面Oxy在竖直平面内，y轴竖直向上，在第一象限内分布着方向竖直向上的匀强电场(不包含y轴)，场强大小用E1，表示，在第二象限内分布着方向沿x轴负方向的匀强电场，场强大小用E2表示。用长度为L的绝缘细线将质量为m、电荷量为+q的带电小球(可看成质点)悬挂在P点，P点在y轴上，坐标为((0, 2L)，在P点正下方与P点距离小于L的某点Q钉一钉子。现用外力把小球拉到左侧与P等高处，细线被拉直与x轴平打，由静止释放，小球运动到最低点时绳恰被拉断，然后进入第一象限，经过时间
，立即在第一象限内再加垂直于Oxy平面向里的匀强磁场(图中未画出)，磁感应强度为
，再经过时间to，=撤去匀强磁场。已知E1=
，E2=
，细线能够承受的最大拉力是F0=3mg。(结果用g、L、m表示)求：
(1)小球在下摆过程中的最大速度vm=?
(2)Q点与P点之间的距离h=?
(3)小球在第一象限运动的时间t=? 小球离开第一象限的位置坐标?
解：
(1) 小球在向下摆动过程中，设合力与竖直方向的夹角为θ，当速度方向与合力方向垂直时，即细线与竖直方向的夹角为θ时，速度最大，设为vm，则
…………………（2分）
解得
，θ=37°
由动能定理有，有
………………………（2分）
解得 
………………………（1分）
（2）设小球运动到Ｐ点正下方时速度为v1，由动能定理有，有
………………………（2分）
解得 
小球运动到最低点时，细线被钉子挡住，做圆周运动的半径为r，则
根据牛顿第二定律，有
………………………（1分）
………………………（1分）
解得
………………………（1分）
（3）绳被拉断，小球进入第一象限，由于qE1=mg，所以小球沿水平方向做匀速直线运动。经过时间t0，加上匀强磁场后，小球做匀速圆周运动，设半径为R，周期为T，则
………………………（1分）
………………………（1分）
解得 
，
所以，
………………………（1分）
即小球做圆周运动时间是四分之三个周期，撤去匀强磁场后，小球向下做匀速直线运动穿过x轴，设撤去匀强磁场时，小球的位置与x轴的距离是y，运动时间为t1，则
………………………（1分）
………………………（1分）
在第一象限的总时间
………………………（1分）
…………（1分）
设小球离开x轴的坐标为（x，0），则
…………（1分）
解得
，小球离开第一象限的位置坐标是（
…（1分）
 |
阅读快车系列答案
在“研究平抛物体的运动”的实验中：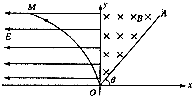
如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky2（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
