题目内容
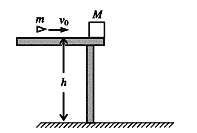
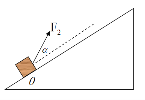
【题目】（18分） 如图所示，金属导轨MNC和PQD，MN与PQ平行且间距为L，所在平面与水平面夹角为α，N、Q连线与MN垂直，M、P间接有阻值为R的电阻；光滑直导轨NC和QD在同一水平面内，与NQ的夹角都为锐角θ。均匀金属棒ab和ef质量均为m，长均为L，ab棒初始位置在水平导轨上与NQ重合；ef棒垂直放在倾斜导轨上，与导轨间的动摩擦因数为μ（μ较小），由导轨上的小立柱1和2阻挡而静止。空间有方向竖直的匀强磁场（图中未画出）。两金属棒与导轨保持良好接触。不计所有导轨和ab棒的电阻，ef棒的阻值为R，最大静摩擦力与滑动摩擦力大小相等，忽略感应电流产生的磁场，重力加速度为g。
（1）若磁感应强度大小为B，给ab棒一个垂直于NQ、水平向右的速度v1，在水平导轨上沿运动方向滑行一段距离后停止，ef棒始终静止，求此过程ef棒上产生的热量；
（2）在（1）问过程中，ab棒滑行距离为d，求通过ab棒某横截面的电荷量；
（3）若ab棒以垂直于NQ的速度v2在水平导轨上向右匀速运动，并在NQ位置时取走小立柱1和2，且运动过程中ef棒始终静止。求此状态下最强磁场的磁感应强度及此磁场下ab棒运动的最大距离。
【答案】（1）Qef＝
；（2）q＝
；（3）Bm＝
，方向竖直向上或竖直向下均可，xm＝
【解析】（1）由于ab棒做切割磁感线运动，回路中产出感应电流，感应电流流经电阻R和ef棒时，电流做功，产生焦耳热，根据功能关系及能的转化与守恒有：
＝QR＋Qef①
根据并联电路特点和焦耳定律Q＝I2Rt可知，电阻R和ef棒中产生的焦耳热相等，即QR＝Qef②
由①②式联立解得ef棒上产生的热量为：Qef＝
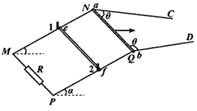
（2）设在ab棒滑行距离为d时所用时间为t，其示意图如下图所示：
该过程中回路变化的面积为：ΔS＝
[L＋（L－2dcotθ）]d ③
根据法拉第电磁感应定律可知，在该过程中，回路中的平均感应电动势为：
＝
④
根据闭合电路欧姆定律可知，流经ab棒平均电流为：
＝
⑤
根据电流的定义式可知，在该过程中，流经ab棒某横截面的电荷量为：q＝
⑥
由③④⑤⑥式联立解得：q＝
（3）由法拉第电磁感应定律可知，当ab棒滑行x距离时，回路中的感应电动势为：e＝B（L－2xcotθ）v2⑦
根据闭合电路欧姆定律可知，流经ef棒的电流为：i＝
⑧
根据安培力大小计算公式可知，ef棒所受安培力为：F＝iLB ⑨
由⑦⑧⑨式联立解得：F＝
⑩
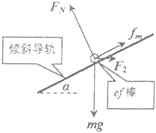
由⑩式可知，当x＝0且B取最大值，即B＝Bm时，F有最大值Fm，ef棒受力示意图如下图所示：
根据共点力平衡条件可知，在沿导轨方向上有：Fmcosα＝mgsinα＋fm
在垂直于导轨方向上有：FN＝mgcosα＋Fmsinα
根据滑动摩擦定律和题设条件有：fm＝μFN
由⑩式联立解得：Bm＝
显然此时，磁感应强度的方向竖直向上或竖直向下均可
由⑩式可知，当B＝Bm时，F随x的增大而减小，即当F最小为Fmin时，x有最大值为xm，此时ef棒受力示意图如下图所示：
根据共点力平衡条件可知，在沿导轨方向上有：Fmincosα＋fm＝mgsinα
在垂直于导轨方向上有：FN＝mgcosα＋Fminsinα
由⑩式联立解得：xm＝
