题目内容
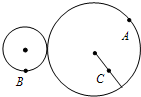
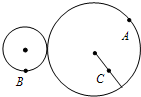如图所示，大轮的半径是小轮的2倍，它们之间靠摩擦传动，接触面不打滑． A、B两点分别位于大、小轮的边缘上，C点位于大轮半径的中点，下列关于这三点的线速度v、角速度ω的说法中，正确的是（ ）分析：两轮靠摩擦传动，轮子边缘上的点线速度大小相等，共轴转动角速度大小相等，根据v=rω求出角速度大小之比和线速度大小之比．
解答：解：A、A、B两点在相等时间内通过的弧长相等，则A、B线速度大小相等．故A错误．
B、A、C两点的角速度大小相等，根据v=rω知，A的线速度是C的2倍．故B正确，D错误．
C、根据ω=
知，A的半径是B的半径的2倍，则A的角速度是B的角速度的一半．故C错误．
故选B．
B、A、C两点的角速度大小相等，根据v=rω知，A的线速度是C的2倍．故B正确，D错误．
C、根据ω=
| v |
| r |
故选B．
点评：解决本题的关键知道靠摩擦传到轮子上的各点线速度大小相等，共轴转动的各点角速度大小相等．
练习册系列答案
相关题目
一皮带传动装置如图所示，右轮的半径为r，a是它边缘上的一点．左侧是一轮轴，大轮的半径为4r，小轮的半径为2r，b点在小轮上，到小轮中心的距离为r，c点和d点分别位于小轮和大轮的边缘上，若在传动过程中皮带不打滑，则（ ）
