题目内容
2.我国的“嫦娥二号”卫星已于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空,取得了圆满成功.这次发射与“嫦娥一号”大为不同,它是由火箭直接发射到地月转移轨道后被月球“俘获”而进入较大的绕月椭圆轨道,又经三次点火制动“刹车”后进入近月圆轨道,在贴近月球表面的近月圆轨道上运行的周期为118分钟,又知道月球表面的重力加速度是地球表面重力加速度的1/6,万有引力常量为G,地球表面重力加速度为g=10m/s2,仅利用以上数据可以计算出( )| A. | 月球对“嫦娥二号”的引力 | B. | 月球上的第一宇宙速度 | ||
| C. | 月球的质量和密度 | D. | “嫦娥二号”的质量 |
分析 卫星在近月圆轨道上绕月运行时,向心加速度近似等于月球表面的重力加速度,由a=$\frac{4{π}^{2}R}{T}$,可求得月球的半径,月球上的第一宇宙速度即为近月卫星的速度,由圆周运动的规律求解;根据万有引力等于向心力列式,分析能否求出月球的质量和密度.
解答 解:卫星在近月圆轨道上绕月运行时,由重力提供向心力,则向心加速度近似等于月球表面的重力加速度,由a=$\frac{4{π}^{2}R}{T}$,已知T,a=$\frac{1}{6}$g,可求得月球的半径;
A、因为不知道嫦娥二号的质量,故无法求得月球对嫦娥二号的引力,故A错误;
B、月球上的第一宇宙速度即为近月卫星的速度,设为v.则 v=$\frac{2πR}{T}$,T已知,R由上可求出,所以可以求出月球上的第一宇宙速度,故B正确;
C、根据万有引力等于向心力,得:G$\frac{mM}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$,得月球的质量:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,可求得月球的质量M,并能求出月球的密度.故C正确;
D、根据万有引力提供圆周运动向心力可求得中心天体的质量,不可以求出环绕天体的质量,故D错误.
故选:BC
点评 本题要建立卫星运动的模型,抓住万有引力充当向心力以及圆周运动的知识结合进行求解

练习册系列答案
相关题目
12.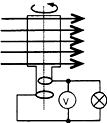 如图为一小型交流发电机模型,N匝线圈的总电阻为lΩ,t=0时刻,线圈平面与磁场平行,它绕垂直于磁场的轴每秒转动50圈,恰能使“8V,16W”的小电珠正常发光.则以下说法正确的是( )
如图为一小型交流发电机模型,N匝线圈的总电阻为lΩ,t=0时刻,线圈平面与磁场平行,它绕垂直于磁场的轴每秒转动50圈,恰能使“8V,16W”的小电珠正常发光.则以下说法正确的是( )
 如图为一小型交流发电机模型,N匝线圈的总电阻为lΩ,t=0时刻,线圈平面与磁场平行,它绕垂直于磁场的轴每秒转动50圈,恰能使“8V,16W”的小电珠正常发光.则以下说法正确的是( )
如图为一小型交流发电机模型,N匝线圈的总电阻为lΩ,t=0时刻,线圈平面与磁场平行,它绕垂直于磁场的轴每秒转动50圈,恰能使“8V,16W”的小电珠正常发光.则以下说法正确的是( )| A. | 电压表的读数为8v | |
| B. | 电压表的读数随时间周期性变化 | |
| C. | 线圈中感应电动势的瞬时值表达式为e=l0cosl00πt V | |
| D. | 该发电机每分钟产生的电能为1200J |
10.下列关于力的说法中正确的是( )?
| A. | 力可以用天平测量? | |
| B. | 只有直接接触的物体间才有力的作用 | |
| C. | 力是不能离开物体而独立存在的 | |
| D. | 拉力、压力、支持力是效果力 |
17.图甲为磁带录音机的磁带盒,可简化为图乙所示的传动模型,A、B为缠绕磁带的两个轮子,两轮的半径均为r,在放音结束时,磁带全部绕到了B轮上,磁带的外缘半径R=3r,现在进行倒带,使磁带绕到A轮上.倒带时A轮是主动轮,其角速度是恒定的,B轮是从动轮,则在倒带的过程中下列说法正确的是( )

| A. | 倒带结束时A、B两轮的角速度之比为1:3 | |
| B. | 倒带开始时A、B两轮的角速度之比为1:3 | |
| C. | 倒带过程中磁带边缘的线速度变小 | |
| D. | 倒带过程中磁带边缘的线速度不变 |
7. 如图所示,木板绕固定的水平轴 O 从水平位置 OA 缓慢转到 OB 位置,木板上的物块始终相对于木板静止,分别用 FN和F f表示物块受到的支持力和摩擦力,在此过程中,以下判断正确的是( )
如图所示,木板绕固定的水平轴 O 从水平位置 OA 缓慢转到 OB 位置,木板上的物块始终相对于木板静止,分别用 FN和F f表示物块受到的支持力和摩擦力,在此过程中,以下判断正确的是( )
 如图所示,木板绕固定的水平轴 O 从水平位置 OA 缓慢转到 OB 位置,木板上的物块始终相对于木板静止,分别用 FN和F f表示物块受到的支持力和摩擦力,在此过程中,以下判断正确的是( )
如图所示,木板绕固定的水平轴 O 从水平位置 OA 缓慢转到 OB 位置,木板上的物块始终相对于木板静止,分别用 FN和F f表示物块受到的支持力和摩擦力,在此过程中,以下判断正确的是( )| A. | FN 和 F f对物块都不做功 | |
| B. | FN 对物块做正功,F f 对物块做负功 | |
| C. | FN 对物块做正功,F f 对物块不做功 | |
| D. | FN 对物块不做功,F f 对物块做正功 |
14.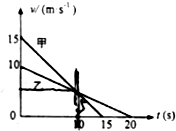 如图是在高速公路上甲、乙两车刹车的v-t图象,甲车在后,乙车在前,若两车发生追尾,则以下判断正确的是( )
如图是在高速公路上甲、乙两车刹车的v-t图象,甲车在后,乙车在前,若两车发生追尾,则以下判断正确的是( )
 如图是在高速公路上甲、乙两车刹车的v-t图象,甲车在后,乙车在前,若两车发生追尾,则以下判断正确的是( )
如图是在高速公路上甲、乙两车刹车的v-t图象,甲车在后,乙车在前,若两车发生追尾,则以下判断正确的是( )| A. | t=0时刻两车间距一定小于12.5m | |
| B. | 甲车刹车的加速度大小是乙车的3倍 | |
| C. | 两车一定是在t=10s之前的某时刻发生追尾 | |
| D. | 两车一定是在t=15s至t=20s之间的某时刻发生追尾 |
11. 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电流的电动势随时间变化的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电流的电动势随时间变化的图象如图乙所示,则( )
 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电流的电动势随时间变化的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电流的电动势随时间变化的图象如图乙所示,则( )| A. | t=0.005 s时线框平面与中性面重合 | |
| B. | t=0.01 s时线框平面与中性面重合 | |
| C. | 线框产生的交变电动势有效值为311 V | |
| D. | 在1秒内,线框在磁场中转100圈 |
5.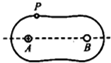 如图所示,一个由绝缘材料制成的闭合环水平放置,环上各点在同一平面内,在环面内A、B两点分别固定两个点电荷QA和QB,其中QA为正电荷,一个带正电的小球P穿在环上,可以沿着闭合环无摩擦滑动,现给小球P一定的初速度,小球恰好能沿环做速度大小不变的运动,则下列判断正确的是( )
如图所示,一个由绝缘材料制成的闭合环水平放置,环上各点在同一平面内,在环面内A、B两点分别固定两个点电荷QA和QB,其中QA为正电荷,一个带正电的小球P穿在环上,可以沿着闭合环无摩擦滑动,现给小球P一定的初速度,小球恰好能沿环做速度大小不变的运动,则下列判断正确的是( )
 如图所示,一个由绝缘材料制成的闭合环水平放置,环上各点在同一平面内,在环面内A、B两点分别固定两个点电荷QA和QB,其中QA为正电荷,一个带正电的小球P穿在环上,可以沿着闭合环无摩擦滑动,现给小球P一定的初速度,小球恰好能沿环做速度大小不变的运动,则下列判断正确的是( )
如图所示,一个由绝缘材料制成的闭合环水平放置,环上各点在同一平面内,在环面内A、B两点分别固定两个点电荷QA和QB,其中QA为正电荷,一个带正电的小球P穿在环上,可以沿着闭合环无摩擦滑动,现给小球P一定的初速度,小球恰好能沿环做速度大小不变的运动,则下列判断正确的是( )| A. | B点固定的电荷QB一定为负电荷 | |
| B. | B点固定的电荷QB一定为正电荷 | |
| C. | QA和QB所产生的电场,在环上各点的电场强度都相同 | |
| D. | QA和QB所产生的电场,在环上各点的电势都相等 |
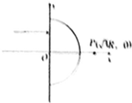 如图所示为一半径为R,折射率n=$\sqrt{3}$的半圆形棱镜,以该半圆形棱镜的直径为y轴,圆心为原点建立直角坐标系,一束平行于x轴的光线垂直射入棱镜,其中某一条光线经过折射后恰好到达x轴上的P点($\sqrt{3}$R,0),求该入射光线距x轴的距离.
如图所示为一半径为R,折射率n=$\sqrt{3}$的半圆形棱镜,以该半圆形棱镜的直径为y轴,圆心为原点建立直角坐标系,一束平行于x轴的光线垂直射入棱镜,其中某一条光线经过折射后恰好到达x轴上的P点($\sqrt{3}$R,0),求该入射光线距x轴的距离.