题目内容
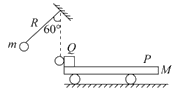
【题目】如图所示,质量为M的平板车P,放在粗糙的地面上,质量为m的小物块Q的大小不计,位于平板车的左端,且M=m=5kg,系统原来静止在水平地面上。一不可伸长的轻质细绳长为R=1.6m,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计)。今将小球拉至悬线与竖直位置成60°角,由静止释放,小球到达最低点时与Q的碰撞时间极短,且无能量损失。已知Q恰能滑到平板车的右端,Q与P之间的动摩擦因数为μ1=0.5,P与地面之间的动摩擦因数为μ2=0.1,重力加速度为g=10m/s2.,若当Q滑到P板的右端时,在P木板上施加一个水平向右的力F,大小为70N,求:
(1)小球到达最低点与Q碰撞之前瞬间的速度v0大小和碰完之后物块Q的瞬时速度大小各为多少;
(2)平板车P的长度L为多少;
(3) 从小物块Q开始滑动到力F作用1s的整个过程中生的热量为多少焦耳。
【答案】(1) 4m/s;4m/s;(2) 1m;(3) 103.75J。
【解析】
(1)小球运动到最低点过程,机械能守恒
![]()
得出
v0=4m/s
小球与物块Q相撞时,没有能量损失,满足动量守恒,机械能守恒,则知
![]()
![]()
由以上两式可以知道二者交换速度
![]()
![]()
(2)小物块Q在平板车P上滑行的过程中
μ1mg=ma1
μ1mg-μ2(M+m)g=Ma2
经t1达到共速v
v=vQ- a1 t1
v=a2t1
SQ1= vQt1-![]() a1t12
a1t12
Sp1= ![]() a2t12
a2t12
L= SQ1- Sp1=1m
(3)施加力F之后,假设板块整体一起走
F-μ2(M+m)g=(M+m)a0
μ1mg=ma1
得出a0> a1 故Q与P分别加速向右运动而直到分离,各自的加速的分别为 a1和 a3
F-μ2(M+m)g-μ1mg =Ma3
设经过t2时间滑离
SQ2= vt2+![]() a1t22
a1t22
Sp2=vt2 + ![]() a3t22
a3t22
L= SP2- SQ2
得出时间
t2=1s
(4)从滑块Q开始滑动到滑离木板全过程生的热量Q为
![]()
得出
Q=103.75J

 名校课堂系列答案
名校课堂系列答案