题目内容
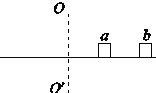
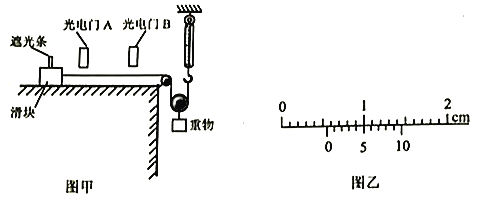
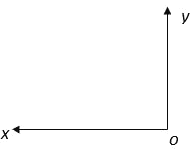
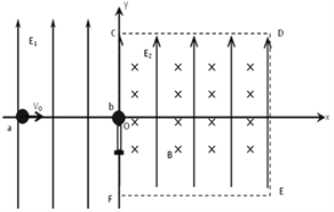
【题目】如图所示,在空间坐标系x<0区域中有竖直向上的匀强电场E1,在一、四象限的正方形区域CDEF内有方向如图所示的正交的匀强电场E2和匀强磁场B,已知CD=2L,OC=L,E2=4E1.在-x轴上有一质量为m、电量为+q的金属a球以速度v0沿x轴向右匀速运动,并与静止在坐标原点O处用绝缘细支柱支撑的(支柱与b球不粘连、无摩擦)质量为2m、不带电金属b球发生弹性碰撞。已知a、b球体积大小、材料相同且都可视为点电荷,碰后电荷总量均分,重力加速度为g,不计a、b球间的静电力,不计a、b球产生的场对电场、磁场的影响,求:
(1)碰撞后,a、b两球的速度大小;
(2)a、b碰后,若b球从CD边界射出,求b球运动时间的范围;
(3)若将磁场反向,两球可否再次碰撞,若可以,请求出磁感应强度;若不可以,请简述理由.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)a匀速运动,则:mg=qE1
ab碰撞,由动量守恒定律得:mv0=mva+2mvb
碰撞过程由能量守恒得:![]()
联立解得:![]()
(2)碰撞后,b受到的电场力为:F电![]()
故b做匀速圆周运动,由牛顿第二定律得:![]()
解得:![]()
若b恰好从C射出,则:L=2r
联立解得:![]()
![]()
若b恰好从D射出,则由几何关系得:r2=4L2+(r﹣L)2
解得:![]()
联立解得:![]()
![]()
故若b从CD边界射出,则其在磁场中运动时间满足:![]()
(3)碰后a、b电量总量平分,即:![]()
碰后a在电场中向左做类平抛运动,b在垂直纸面向外的磁场中偏转半周再进入电场中做类平抛运动,设两球再次相遇的位置在P点,其坐标为(-x,-y)
根据类平抛运动x=vt
则类平抛运动时间差满足![]()
由牛顿第二定律得球a : ![]() a
a
同理球b: ![]()
解得![]()
根据类平抛运动 ![]()
则类平抛运动的侧向位移差满足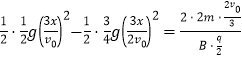
联立方程得![]()

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目