题目内容
如图所示,一平板车以速度 v0=5m/s 在水平路面匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为 l=3
m,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做 a1=3m/s2 的匀减速直线运动.已知货箱与平板车之间的摩擦因数为 μ=0.2,g=10m/s2.求:
(1)货箱刚放上平板车瞬间,货箱的加速度大小和方向;
(2)货箱放到车上开始计时,经过多少时间货箱与平板车速度相同;
(3)如果货箱不能掉下,则最终停止时离车后端的距离 d 是多少.
| 1 | 6 |

(1)货箱刚放上平板车瞬间,货箱的加速度大小和方向;
(2)货箱放到车上开始计时,经过多少时间货箱与平板车速度相同;
(3)如果货箱不能掉下,则最终停止时离车后端的距离 d 是多少.
分析:(1)货箱刚放上平板车瞬间,货箱相对平板车向左运动,滑动摩擦力提供加速度,根据牛顿第二定律即可求解;
(2)货箱放到车上后,先做匀加速运动,根据速度时间公式即可求解时间;
(3)由于货箱的最大加速度 a1=μg=2m/s2<a1,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止.根据匀变速运动基本公式即可求出距离d.
(2)货箱放到车上后,先做匀加速运动,根据速度时间公式即可求解时间;
(3)由于货箱的最大加速度 a1=μg=2m/s2<a1,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止.根据匀变速运动基本公式即可求出距离d.
解答:解:(1)货箱刚放上平板车瞬间,货箱相对平板车向左运动,由μmg=ma,得a=μg=2 m/s2,方向与车前进方向相同
(2)货箱放到车上后,先做匀加速运动,设经过时间 t和车达到相同速度,
由at=vo-a1t
得t=1s
(3)当货箱和车速度相等,此时货箱和车的位移分别为 x1、x2,
对货箱:x1=vot-
a1t2
对平板车:x2=vot-
at2
此时,货箱相对车向后移动了△x=x2-x1=2.5 m<l=3
m,货箱不会从车后端掉下来.
由于货箱的最大加速度 a=μg=2 m/s2<a1,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止,此时相同速度为 v=a1t=2 m/s
对货箱:s1=
=1 m
对平板车:s2=
=
m
故货箱到车尾的距离 d=l-△x+s1-s2=1 m;
答:(1)货箱刚放上平板车瞬间,货箱的加速度大小为2 m/s2,方向与车前进方向相同;
(2)货箱放到车上开始计时,经过1s的时间货箱与平板车速度相同;
(3)如果货箱不能掉下,则最终停止时离车后端的距离是1m.
(2)货箱放到车上后,先做匀加速运动,设经过时间 t和车达到相同速度,
由at=vo-a1t
得t=1s
(3)当货箱和车速度相等,此时货箱和车的位移分别为 x1、x2,
对货箱:x1=vot-
| 1 |
| 2 |
对平板车:x2=vot-
| 1 |
| 2 |
此时,货箱相对车向后移动了△x=x2-x1=2.5 m<l=3
| 1 |
| 6 |
由于货箱的最大加速度 a=μg=2 m/s2<a1,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止,此时相同速度为 v=a1t=2 m/s
对货箱:s1=
| v2 |
| 2a1 |
对平板车:s2=
| v2 |
| 2a |
| 2 |
| 3 |
故货箱到车尾的距离 d=l-△x+s1-s2=1 m;
答:(1)货箱刚放上平板车瞬间,货箱的加速度大小为2 m/s2,方向与车前进方向相同;
(2)货箱放到车上开始计时,经过1s的时间货箱与平板车速度相同;
(3)如果货箱不能掉下,则最终停止时离车后端的距离是1m.
点评:本题是相对运动的题目,要对每个物体分别分析其运动情况,利用运动学的基本公式,再根据速度和位移的关系求解,本题运动过程较为复杂,难度较大.

练习册系列答案
相关题目
 如图所示,一平板车以某一速度 vo=5m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为 l=
如图所示,一平板车以某一速度 vo=5m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为 l= (2006?武汉模拟)如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
(2006?武汉模拟)如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件? 如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速地放置于平板车上,货箱离车后端的距离为l=3m,货箱放在车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数μ=0.2,g取10m/s2,
如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速地放置于平板车上,货箱离车后端的距离为l=3m,货箱放在车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数μ=0.2,g取10m/s2, 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为
匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为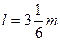 ,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做
,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做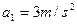 的匀减速直线运动。已知货箱与平板车之间的摩擦因数为
的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 。求:
。求: 是多少?
是多少? 的加速度匀加速直线运动,经过3秒,货箱距离车后端多远?已知平板车后端离地面高1.25m,货箱落地后不动。
的加速度匀加速直线运动,经过3秒,货箱距离车后端多远?已知平板车后端离地面高1.25m,货箱落地后不动。