题目内容
 如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速地放置于平板车上,货箱离车后端的距离为l=3m,货箱放在车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数μ=0.2,g取10m/s2,
如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速地放置于平板车上,货箱离车后端的距离为l=3m,货箱放在车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数μ=0.2,g取10m/s2,(1)求平板车开始刹车时,货箱加速度?
(2)为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
(3)若v0=4m/s时平板车从开始刹车到最后静止的全过程中,平板车相对地面的位移和平板车相对于货箱的位移以及路程各为多少?
分析:(1)对货箱由牛顿第二定律可以求出其加速度;
(2)货箱先相对平板车向左滑,当与平板车的速度相等后相对平板车向右滑.若货箱与平板车的速度相等时,货箱仍未从平板车上掉下来,则以后货箱不会从平板上掉下来.
(3)平板车从开始刹车到最后静止的全过程中,小车一直做匀减速运动,货物放到车上,先匀加速后匀减速,根据运动学公式列式联立可求解相对位移与路程.
(2)货箱先相对平板车向左滑,当与平板车的速度相等后相对平板车向右滑.若货箱与平板车的速度相等时,货箱仍未从平板车上掉下来,则以后货箱不会从平板上掉下来.
(3)平板车从开始刹车到最后静止的全过程中,小车一直做匀减速运动,货物放到车上,先匀加速后匀减速,根据运动学公式列式联立可求解相对位移与路程.
解答:解:(1)对货箱由牛顿第二定律得:μmg=ma1,加速度a1=μg=0.2×10=2m/s2;
(2)设经过时间t,货箱和平板车达到共同速度v,
货箱向右运动的位移:S箱=
a1t2
又:v=a1 t
平板车向右运动的位移:S车=v0t-
at2
又:v=v0-a t
为使货箱不从平板车上掉下来,应满足:S箱+L≥S车
联立上述各式,解得:v0≤
代入数据:v0≤6m/s
(3)小车一直做匀减速运动,平板车相对于地面的位移s车=
=
=2m;
货物放到车上,先匀加速后匀减速,加速度a1=2m/s2
当和平板车具有共同速度时,时间为t1
4-4t1=2t1
解得:t1=
s,
s之前货物做匀加速,之后做匀减速,共同速度之前相对位移△x1=
×4×
=
m
共同速度之后相对位移:△x2=
×1×
=
m
故相对位移△x=△x1-△x2=
-
=
m
相对路程:△s=
+
=
m
答:(1)平板车开始刹车时,货箱加速度为2m/s2;
(2)为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足:v0≤6m/s
(3)平板车相对地面的位移和平板车相对于货箱的位移为
m,路程为
m
(2)设经过时间t,货箱和平板车达到共同速度v,
货箱向右运动的位移:S箱=
| 1 |
| 2 |
又:v=a1 t
平板车向右运动的位移:S车=v0t-
| 1 |
| 2 |
又:v=v0-a t
为使货箱不从平板车上掉下来,应满足:S箱+L≥S车
联立上述各式,解得:v0≤
| 2(a+a1)l |
代入数据:v0≤6m/s
(3)小车一直做匀减速运动,平板车相对于地面的位移s车=
| ||
| 2a |
| 42 |
| 2×4 |
货物放到车上,先匀加速后匀减速,加速度a1=2m/s2
当和平板车具有共同速度时,时间为t1
4-4t1=2t1
解得:t1=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
共同速度之后相对位移:△x2=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
故相对位移△x=△x1-△x2=
| 4 |
| 3 |
| 1 |
| 6 |
| 7 |
| 6 |
相对路程:△s=
| 4 |
| 3 |
| 1 |
| 6 |
| 3 |
| 2 |
答:(1)平板车开始刹车时,货箱加速度为2m/s2;
(2)为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足:v0≤6m/s
(3)平板车相对地面的位移和平板车相对于货箱的位移为
| 7 |
| 6 |
| 3 |
| 2 |
点评:本题是相对运动的题目,要对每个物体分别分析其运动情况,利用运动学的基本公式,再根据速度和位移的关系求解,本题运动过程较为复杂,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图所示,一平板车以某一速度 vo=5m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为 l=
如图所示,一平板车以某一速度 vo=5m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为 l= (2006?武汉模拟)如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
(2006?武汉模拟)如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件? 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为
匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为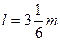 ,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做
,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做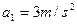 的匀减速直线运动。已知货箱与平板车之间的摩擦因数为
的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 。求:
。求: 是多少?
是多少? 的加速度匀加速直线运动,经过3秒,货箱距离车后端多远?已知平板车后端离地面高1.25m,货箱落地后不动。
的加速度匀加速直线运动,经过3秒,货箱距离车后端多远?已知平板车后端离地面高1.25m,货箱落地后不动。