题目内容
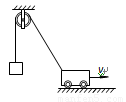
 如图所示,绕过定滑轮的细绳一端拴在小车上,另一端吊一物体A,若小车沿水平地面向前匀速运动,则物体( )
如图所示,绕过定滑轮的细绳一端拴在小车上,另一端吊一物体A,若小车沿水平地面向前匀速运动,则物体( )分析:由题小车做匀速运动,将小车的运动分解为沿绳子方向的运动,以及垂直绳子方向运动即绕滑轮的转动,得到沿绳子方向的运动速度,即物体A的速度表达式,运用平行四边形定则作出v的分解图,根据三角函数来确定A的瞬时速度,即可分析A的速度如何变化.
解答:解:设任一时刻绳子与水平方向的夹角为θ,A的瞬时速度大小为vA.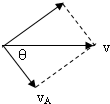
将小车的运动分解为沿绳子方向的运动,以及垂直绳子方向的运动,即绕滑轮的转动,如图,则由三角函数可解得:vA=vcosθ
v不变,θ减小,则cosθ增大,故vA增大,即物体A向上做加速运动
故选A

将小车的运动分解为沿绳子方向的运动,以及垂直绳子方向的运动,即绕滑轮的转动,如图,则由三角函数可解得:vA=vcosθ
v不变,θ减小,则cosθ增大,故vA增大,即物体A向上做加速运动
故选A
点评:本题关键是正确地找出小车的合运动与分运动,然后根据运动分解的平行四边形定则,得到物体A速度的一般表达式,即可进行分析其运动情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示,绕过定滑轮的轻绳拴在小车上,另一端吊一物体,若小车沿水平向前匀速运动,则物体的运动状态为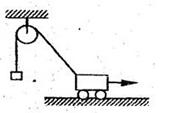
| A.向上做加速运动 |
| B.向上做匀速运动 |
| C.向上做减速运动 |
| D.无法确定 |
 如图所示,绕过定滑轮的绳子,一端系一质量为10kg的物体A,另一端被人握住,最初绳沿竖直方向,手到滑轮距离为3m.之后人握住绳子向前运动,使物体A匀速上升,则在人向前运动4m的过程中,对物体A作的功为
如图所示,绕过定滑轮的绳子,一端系一质量为10kg的物体A,另一端被人握住,最初绳沿竖直方向,手到滑轮距离为3m.之后人握住绳子向前运动,使物体A匀速上升,则在人向前运动4m的过程中,对物体A作的功为