��Ŀ����
����Ϊm��С���ɳ�ΪL��ϸ��ϵס��ϸ�ߵ���һ�˹̶��� A�㣬AB�ǹ�A����ֱ�ߣ���AB=L��EΪAB���е㣬��E��ˮƽ�� EF����EF��ijһλ�ö�һС��D����ͼ��ʾ���ֽ�С����������ˮƽ��Ȼ���ɾ�ֹ�ͷţ��������붤��ײʱ�Ļ�е����ʧ��
��1����������E��λ�ã���С��B��ǰ��˲�䣬���������ֱ�Ϊ���٣�
��2����С��ǡ���ƶ�������ֱƽ������Բ���˶�������D��λ����E��ľ���x��
��3������С��D��λ�ò��䣬��С���ͼʾ��P�㾲ֹ�ͷţ���С���˶�����͵�ʱ����ϸ�߸պôﵽ����������Ͽ������С���˶��Ĺ켣����B�㣮����ϸ���ܳ��ܵ��������T��
��1����������E��λ�ã���С��B��ǰ��˲�䣬���������ֱ�Ϊ���٣�
��2����С��ǡ���ƶ�������ֱƽ������Բ���˶�������D��λ����E��ľ���x��
��3������С��D��λ�ò��䣬��С���ͼʾ��P�㾲ֹ�ͷţ���С���˶�����͵�ʱ����ϸ�߸պôﵽ����������Ͽ������С���˶��Ĺ켣����B�㣮����ϸ���ܳ��ܵ��������T��

��1��С���M�㵽B��Ĺ����У����ݶ��ܶ����ã�
mgL=
mv2
��ǰ��T1-mg=m
��ã�T1=3mg
����T2-mg=m
��ã�T2=5mg
��2��С��ǡ��������ֱƽ������Բ���˶�������ߵ�ʱ���ٶ�v1����ʱ��Բ���˶��İ뾶Ϊr��
��mg��
-r��=
mv12 ��
��mg=m
��
�ɼ��ι�ϵ��x2=��L-r��2-��
��2 ��
��������ʽ�ɵã�
r=
��
x=
L ��
��3��С����Բ���˶�������͵�ʱ���ٶ���Ϊv2��
T-mg=m
��
�Ժ�С����ƽ���˶���B�㣬
��ˮƽ������x=v2t ��
����ֱ�����У�
-r=
gt2 ��
�ɢܢݢޢߢ�ʽ�ɵã�T=
mg
�𣺣�1����������E��λ�ã���С��B��ǰ��˲�䣬���������ֱ�Ϊ3mg��5mg��
��2����С��ǡ���ƶ�������ֱƽ������Բ���˶�������D��λ����E��ľ���xΪ
L��
��3��ϸ���ܳ��ܵ��������TΪ
mg��
mgL=
| 1 |
| 2 |
��ǰ��T1-mg=m
| v2 |
| L |
��ã�T1=3mg
����T2-mg=m
| v2 | ||
(
|
��ã�T2=5mg
��2��С��ǡ��������ֱƽ������Բ���˶�������ߵ�ʱ���ٶ�v1����ʱ��Բ���˶��İ뾶Ϊr��
��mg��
| L |
| 2 |
| 1 |
| 2 |
��mg=m
| ||
| r |
�ɼ��ι�ϵ��x2=��L-r��2-��
| L |
| 2 |
��������ʽ�ɵã�
r=
| L |
| 3 |
x=
| ||
| 6 |
��3��С����Բ���˶�������͵�ʱ���ٶ���Ϊv2��
T-mg=m
| ||
| r |
�Ժ�С����ƽ���˶���B�㣬
��ˮƽ������x=v2t ��
����ֱ�����У�
| L |
| 2 |
| 1 |
| 2 |
�ɢܢݢޢߢ�ʽ�ɵã�T=
| 11 |
| 4 |
�𣺣�1����������E��λ�ã���С��B��ǰ��˲�䣬���������ֱ�Ϊ3mg��5mg��
��2����С��ǡ���ƶ�������ֱƽ������Բ���˶�������D��λ����E��ľ���xΪ
| ||
| 6 |
��3��ϸ���ܳ��ܵ��������TΪ
| 11 |
| 4 |

��ϰ��ϵ�д�
�����Ŀ
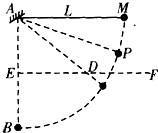 ��2008?��ͨ��ģ������Ϊm��С���ɳ�ΪL��ϸ��ϵס��ϸ�ߵ���һ�˹̶��� A�㣬AB�ǹ�A����ֱ�ߣ���AB=L��EΪAB���е㣬��E��ˮƽ�� EF����EF��ijһλ�ö�һС��D����ͼ��ʾ���ֽ�С����������ˮƽ��Ȼ���ɾ�ֹ�ͷţ��������붤��ײʱ�Ļ�е����ʧ��
��2008?��ͨ��ģ������Ϊm��С���ɳ�ΪL��ϸ��ϵס��ϸ�ߵ���һ�˹̶��� A�㣬AB�ǹ�A����ֱ�ߣ���AB=L��EΪAB���е㣬��E��ˮƽ�� EF����EF��ijһλ�ö�һС��D����ͼ��ʾ���ֽ�С����������ˮƽ��Ȼ���ɾ�ֹ�ͷţ��������붤��ײʱ�Ļ�е����ʧ�� ��ͼ��ʾ��һ������Ϊm��С��������ϸ��˩����ֱת���ϵ�A��B������AB���ΪL��A������Ϊ
��ͼ��ʾ��һ������Ϊm��С��������ϸ��˩����ֱת���ϵ�A��B������AB���ΪL��A������Ϊ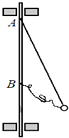 ��ͼ��ʾ��һ������Ϊm��С��������ϸ��˩����ֱת���ϵ�A��B������AB���ΪL��A������Ϊ
��ͼ��ʾ��һ������Ϊm��С��������ϸ��˩����ֱת���ϵ�A��B������AB���ΪL��A������Ϊ