题目内容
在光滑水平面上有一质量m=1.0×10-3kg,电量q=1.0×10-10C的带正电小球静止在O点,以O点为原点,在该水平面内建立直角坐标系Oxy,现突然加一沿x轴正方向,场强大小E=2.0×106V/m的匀强电场,使小球开始运动经过1.0s,所加电场突然变为沿y轴正方向,场强大小仍为E=2.0×106V/m的匀强电场再经过1.0s,所加电场又突然变为另一个匀强电场,使小球在此电场作用下经1.0s速度变为零.求此电场的方向及速度变为零时小球的位置.
分析:分析小球的运动情况:第1s内小球沿x轴正方向做匀加速直线运动,第2s内做类平抛运动,加速度沿y轴正方向,第3s内做匀减速直线运动.根据牛顿第二定律和运动学公式求出第1s末小球的速度和位移.对于类平抛运动,运用运动的分解法求出第2秒末小球的速度大小和方向,并求出x方向和y方向的位移大小.再根据牛顿第二定律和运动学公式求出电场的方向和第3s末的位置.
解答:解:由牛顿第二定律得知,在匀强电场中小球加速度的大小恒为:a=
代入数值得:a=
m/s2=0.20m/s2
第1s内:场强沿x正方向时,经过1秒钟小球的速度大小为:
Vx=at=0.20×1.0=0.20m/s
速度的方向沿x轴正方向,小球沿x轴方向移动的距离
△x1=
at2=
×0.20×1.02=0.10m
第2秒内:电场方向沿y轴正方向,故小球在x方向做速度为Vx的匀速运动,在y方向做初速为零的匀加速运动,
沿x方向移动的距离:△x2=Vxt=0.20m
沿y方向移动的距离:△y=
at2=
×0.20×1.02=0.10m
故在第2秒末小球到达的位置坐标:x2=△x1+△x2=0.30m
y2=△y=0.10m
在第2秒末小球在x方向的分速度仍为Vx,在y方向的分速度为
Vy=at=0.20×1.0=0.20m/s
由上可知,此时运动方向与x轴成45°角.要使小球速度能变为零,则在第3秒内所加匀强电场的方向必须与此方向相反,即指向第三象限,与x轴成225°角.
第3秒内:设在电场作用下小球加速度的x分量和y分量分别为ax,ay,则
ax=
=0.20m/s2,
ay=
=0.20m/s2
在第3秒未小球到达的位置坐标为
x3=x2+Vxt-
axt2=0.40m,
y3=y2+Vyt-
ayt2=0.20m
答:此电场的方向为指向第三象限,与x轴成225°角.速度变为零时小球的位置为x3=0.40m,y3=0.20m.
| qE |
| m |
代入数值得:a=
| 1.0×10-10×2.0×106 |
| 1.0×10-3 |
第1s内:场强沿x正方向时,经过1秒钟小球的速度大小为:
Vx=at=0.20×1.0=0.20m/s
速度的方向沿x轴正方向,小球沿x轴方向移动的距离
△x1=
| 1 |
| 2 |
| 1 |
| 2 |
第2秒内:电场方向沿y轴正方向,故小球在x方向做速度为Vx的匀速运动,在y方向做初速为零的匀加速运动,
沿x方向移动的距离:△x2=Vxt=0.20m
沿y方向移动的距离:△y=
| 1 |
| 2 |
| 1 |
| 2 |
故在第2秒末小球到达的位置坐标:x2=△x1+△x2=0.30m
y2=△y=0.10m
在第2秒末小球在x方向的分速度仍为Vx,在y方向的分速度为
Vy=at=0.20×1.0=0.20m/s
由上可知,此时运动方向与x轴成45°角.要使小球速度能变为零,则在第3秒内所加匀强电场的方向必须与此方向相反,即指向第三象限,与x轴成225°角.
第3秒内:设在电场作用下小球加速度的x分量和y分量分别为ax,ay,则
ax=
| Vx |
| t |
ay=
| Vy |
| t |
在第3秒未小球到达的位置坐标为
x3=x2+Vxt-
| 1 |
| 2 |
y3=y2+Vyt-
| 1 |
| 2 |
答:此电场的方向为指向第三象限,与x轴成225°角.速度变为零时小球的位置为x3=0.40m,y3=0.20m.
点评:本题考查运用牛顿第二定律和运动学公式分析和处理动力学问题,要通过计算进行分析.类平抛运动运用运动的合成与分解的方法研究.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )
在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )| A、物块一直减速至速度为零 | ||
| B、物块的加速度先减小后增大 | ||
| C、当弹力等于F后,物块将静止在水平面上 | ||
D、当物块的速度为零时,弹簧的压缩量等于
|
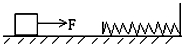 在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )
在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )| A、物块接触弹簧后即做减速运动 | B、物块接触弹簧后先加速后减速 | C、当物块的速度为零时,它所受的合力也为零 | D、当物体加速度为零时,物块的速度也等于零 |
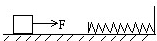 在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( )
在光滑水平面上有一物块受水平恒力F的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触并将弹簧压至最短的过程中,下列说法正确的是( ) 如图所示,在光滑水平面上有一物块在水平恒外力F的作用下从静止开始运动,在其正前方有一根固定在墙上的轻质弹簧,从物块与弹簧接触到弹簧压缩量最大的过程中,下列说法正确的是( )
如图所示,在光滑水平面上有一物块在水平恒外力F的作用下从静止开始运动,在其正前方有一根固定在墙上的轻质弹簧,从物块与弹簧接触到弹簧压缩量最大的过程中,下列说法正确的是( ) 如图,在光滑水平面上有一物块始终受水平向右恒力F的作用而运动,在其正前方固定一个较长的轻质弹簧,则在物块与弹簧接触后向右运动至弹簧压缩到最短的过程中( )
如图,在光滑水平面上有一物块始终受水平向右恒力F的作用而运动,在其正前方固定一个较长的轻质弹簧,则在物块与弹簧接触后向右运动至弹簧压缩到最短的过程中( )