题目内容
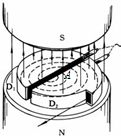 2006年6月23日,中国首台西门子eclipse HP/RD医用回旋加速器在位于广州军区总医院内的正电子药物研发中心正式投入临床运营.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑重力作用.( )
2006年6月23日,中国首台西门子eclipse HP/RD医用回旋加速器在位于广州军区总医院内的正电子药物研发中心正式投入临床运营.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑重力作用.( )A、某粒子第1次和第2次经过两狭缝后的轨道半径之比为1:
| ||
B、粒子从静止开始加速到出口处所需的时间为
| ||
| C、粒子能获得的最大动能Ek加速器磁感应强度无关 | ||
| D、加速电压越大粒子能获得的最大动能Ek大 |
分析:回旋加速器利用电场加速和磁场偏转来加速粒子,带电粒子在磁场中运动的周期与带电粒子的速度无关.根据洛伦兹力提供向心力得出轨道半径的公式,从而根据速度的关系得出轨道半径的关系.粒子离开回旋加速度时的轨道半径等于D形盒的半径,根据半径公式求出离开时的速度大小,从而得出动能.
粒子被电场加速一次动能的增加qU,根据最大动能求出加速的次数,粒子在磁场中运动一个周期被加速两次,从而知道粒子运动的周期次数,从而求出运动的时间.
粒子被电场加速一次动能的增加qU,根据最大动能求出加速的次数,粒子在磁场中运动一个周期被加速两次,从而知道粒子运动的周期次数,从而求出运动的时间.
解答:解:A、根据v2=2ax得,带电粒子第一次和和第二次经过加速后的速度比为
:2,
根据r=
知,带电粒子第1次和第2次经过两D形盒间狭缝后轨道半径之比r1:r2=1:
,故A正确.
B、粒子被电场加速一次动能的增加qU,
则粒子被加速的次数n=
=
粒子在磁场中运动周期的次数n′=
=
T=
则粒子从静止开始到出口处所需的时间t=n′T=
,故B正确.
C、根据qvB=m
,知v=
,
则带电粒子离开回旋加速器时获得动能为Ek=
mv2=
.故CD错误.
故选:AB.
| 2 |
根据r=
| mv |
| Bq |
| 2 |
B、粒子被电场加速一次动能的增加qU,
则粒子被加速的次数n=
| EKM |
| qU |
| qB2R2 |
| 2mU |
粒子在磁场中运动周期的次数n′=
| n |
| 2 |
| qB2R2 |
| 4mU |
T=
| 2πm |
| Bq |
则粒子从静止开始到出口处所需的时间t=n′T=
| πBR2 |
| 2U |
C、根据qvB=m
| v2 |
| R |
| qBR |
| m |
则带电粒子离开回旋加速器时获得动能为Ek=
| 1 |
| 2 |
| B2q2R2 |
| 2m |
故选:AB.
点评:解决本题的关键知道回旋加速器加速粒子的原理,知道带电粒子在磁场中运动的周期与交变电场的周期相同,以及掌握带电粒子在磁场中运动的轨道半径公式和周期公式.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图所示,2006年8月24日晚,国际天文学联合会大会投票,通过了新的行星定义,冥王星被排除在行星行列之外,太阳系行星数量将由九颗减为八颗.若将八大行星绕太阳运行的轨迹粗略地认为是圆,各星球半径和轨道半径如下表所示
如图所示,2006年8月24日晚,国际天文学联合会大会投票,通过了新的行星定义,冥王星被排除在行星行列之外,太阳系行星数量将由九颗减为八颗.若将八大行星绕太阳运行的轨迹粗略地认为是圆,各星球半径和轨道半径如下表所示