题目内容
（供选学物理1-1的考生做）（8分）如图所示，位于竖直平面内的光滑轨道，由一段倾斜直轨道和与之相切的圆形轨道连接而成，圆形轨道的半径为R。
（1）若质量为m的小物块（可视为质点）从倾斜直轨道上距圆轨道最低点高为R处由静止开始下滑，求其滑到圆轨道最低点时的速度大小及所受轨道的支持力大小。
（2）若质量为m的小物块（可视为质点）从倾斜直轨道上距圆轨道最低点高为R处开始以一定的初速度沿倾斜直轨道下滑，要求小物块能通过圆形轨道最高点，且在最高点与轨道间的压力不能超过5mg（g为重力加速度），试分析小物块的初速度应满足什么条件。
（1）设小物块运动至圆轨道最低点时的速度为v1，所受轨道的支持力为FN1，根据机械能守恒定律，对于小物块从开始下滑至轨道最低点的过程有
mgR=
mv12，解得v1=
…………………………………………………………（2分）
根据牛顿第二定律，对于小物块在圆轨道最低点有
FN1-mg=mv12/R，解得FN1=3mg…………………………………………………………（2分）
（2）设小物块恰能通过圆轨道最高点的速度大小为v2，轨道对小物块的压力FN2=5mg时的速度大小为v3，根据牛顿第二定律，对于小物块在最高点的两种情况分别有
mg=mv22/R， FN2+mg=mv32/R……………………………………………………（2分）
解得v22=gR，v32=6gR
设对应上述两种情况下，小物块的初速度分别为v20和v30，对于小物块从开始沿斜轨道下滑到运动至轨道最高点的过程，根据机械能守恒定律分别有
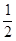mv202=mgR+mv22， mv302=mgR+mv32
解得v20=
，v30=
即小物块的初速度应满足≤v≤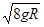 …………………………………………（2分）
解析:略
灵星计算小达人系列答案
孟建平错题本系列答案
，月球的半径约为地球半径的
，地球半径为6400km，地球表面附近的重力加速度为9.8m/s2．求：
，月球的半径约为地球半径的
，地球半径为6400km，地球表面附近的重力加速度为9.8m/s2．求：
，月球的半径约为地球半径的
，地球半径为6400km，地球表面附近的重力加速度为9.8m/s2．求：