题目内容
4.地球绕太阳运行的半长轴为1.5×1011m,周期为365天;月球绕地球运行的轨道半长轴为3.82×108m,周期为27.3天,则对于绕太阳运行的行星;$\frac{{R}^{3}}{{T}^{2}}$的值为3.4×1018m3/s2,对于绕地球运行的物体,则$\frac{{R}^{3}}{{T}^{2}}$=9.8×1012 m3/s2.分析 据开普勤第三定律得环绕天体轨道半长轴的三次方和公转周期的二次方之比为一定值,故根据地球绕太阳运动可以求得绕太阳运行的行星的K值,同理绕地球人的造卫星的K值亦可以由月球绕地球运动求得.
解答 解:1天=24×3600s
地球绕太阳运动的$\frac{{R}^{3}}{{T}^{2}}$=$\frac{(1.50×1{0}^{11})^{3}}{(365×24×3600)^{2}}{m}^{3}/{s}^{2}$=3.4×1018 m3/s2
月球绕地球运动的$\frac{{R}^{3}}{{T}^{2}}$=$\frac{(3.8×1{0}^{8})^{3}}{(27.3×24×3600)^{2}}{m}^{3}/{s}^{2}$=9.8×1012 m3/s2
根据开普勤第三定律可得:绕太阳运动的行星$\frac{{R}^{3}}{{T}^{2}}$=3.4×1018 m3/s2;绕地球运动的卫星$\frac{{R}^{3}}{{T}^{2}}$=9.8×1012 m3/s2.
故答案为:3.4×1018;9.8×1012
点评 注意时间单位的换算,以及比值是有单位的.熟悉开普勒第三定律,由地球得到其它行星绕太阳运动的$\frac{{R}^{3}}{{T}^{2}}$,由月球绕地球运动得到所有卫星绕地于运动的$\frac{{R}^{3}}{{T}^{2}}$.

练习册系列答案
相关题目
14.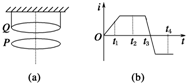 如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
 如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )
如图(a)所示,圆形线圈P静止在水平桌面上,其正上方悬挂一相同线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为FN,则( )| A. | t1时刻FN>G | B. | t2时刻FN>G | C. | t3时刻FN=G | D. | t4时刻FN<G |
15. 两列振幅、波长和波速都相同的简谐波a和b分别沿x轴的正方向、负方向传播,波速v=200m/s,在t=0时刻的部分波形如图所示,那么在x轴上x=450m的质点P,经最短时间t1出现位移最大值,经最短时间t2出现位移最小值,则t1、t2分别是( )
两列振幅、波长和波速都相同的简谐波a和b分别沿x轴的正方向、负方向传播,波速v=200m/s,在t=0时刻的部分波形如图所示,那么在x轴上x=450m的质点P,经最短时间t1出现位移最大值,经最短时间t2出现位移最小值,则t1、t2分别是( )
 两列振幅、波长和波速都相同的简谐波a和b分别沿x轴的正方向、负方向传播,波速v=200m/s,在t=0时刻的部分波形如图所示,那么在x轴上x=450m的质点P,经最短时间t1出现位移最大值,经最短时间t2出现位移最小值,则t1、t2分别是( )
两列振幅、波长和波速都相同的简谐波a和b分别沿x轴的正方向、负方向传播,波速v=200m/s,在t=0时刻的部分波形如图所示,那么在x轴上x=450m的质点P,经最短时间t1出现位移最大值,经最短时间t2出现位移最小值,则t1、t2分别是( )| A. | 1.75s,1.25s | B. | 0.25s,0.75s | C. | 1.25s,0.75s | D. | 0.25s,1.25s |
19. 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )| A. | 加一磁场,磁场方向沿z轴负方向 | B. | 加一磁场,磁场方向沿y轴正方向 | ||
| C. | 加一电场,电场方向沿z轴负方向 | D. | 加一电场,电场方向沿y轴正方向 |
16. 某横波在介质中沿x轴正方向传播,t=0时刻时波源O开始振动,振动方向沿y轴负方向,图示为t=0.7s时的波形图,已知图中b点第二次出现在波谷,则该横波的传播速度v是( )
某横波在介质中沿x轴正方向传播,t=0时刻时波源O开始振动,振动方向沿y轴负方向,图示为t=0.7s时的波形图,已知图中b点第二次出现在波谷,则该横波的传播速度v是( )
 某横波在介质中沿x轴正方向传播,t=0时刻时波源O开始振动,振动方向沿y轴负方向,图示为t=0.7s时的波形图,已知图中b点第二次出现在波谷,则该横波的传播速度v是( )
某横波在介质中沿x轴正方向传播,t=0时刻时波源O开始振动,振动方向沿y轴负方向,图示为t=0.7s时的波形图,已知图中b点第二次出现在波谷,则该横波的传播速度v是( )| A. | $\frac{50}{7}$m/s | B. | 10m/s | C. | $\frac{90}{7}$m/s | D. | $\frac{100}{7}$m/s |
13. 我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接,已知空间站绕月运行的圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法正确的是( )
我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接,已知空间站绕月运行的圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法正确的是( )
 我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接,已知空间站绕月运行的圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法正确的是( )
我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接,已知空间站绕月运行的圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法正确的是( )| A. | 要使对接成功,航天飞机在接近B点时必须加速 | |
| B. | 航天飞机在图示位置正在加速向B运动 | |
| C. | 月球的质量为M=$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | |
| D. | 月球的第一宇宙速度为v=$\frac{2πr}{T}$ |
14.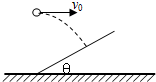 以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是( )(g取9.8m/s2)
以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是( )(g取9.8m/s2)
 以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是( )(g取9.8m/s2)
以9.8m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,可知物体完成这段飞行的时间是( )(g取9.8m/s2)| A. | $\frac{\sqrt{3}}{3}$s | B. | $\frac{2\sqrt{3}}{3}$s | C. | $\sqrt{3}$s | D. | 2 s |