题目内容
12.在光滑水平桌面上停放着A、B小车,其质量mA=2mB,两车中间有一根用细线缚住的被压缩弹簧,当烧断细线弹簧弹开时,A车的动量变化量和B车的动量变化量之比为1:1.分析 系统动量守恒,应用动量守恒定律求出两车的动量变化量之比.
解答 解:桌面光滑,两车组成的系统所受合外力为零,系统动量守恒,
以A的速度方向为正方向,由动量守恒定律得:pA-pB=0,
动量变化量大小之比:$\frac{△{p}_{A}}{△{p}_{B}}$=$\frac{{p}_{A}}{{p}_{B}}$=$\frac{1}{1}$;
故答案为:1:1.
点评 本题考查了求小车动量变化量之比,两小车组成的系统动量守恒,小车的初动量为零,末动量就等于小车动量的变化量,应用动量守恒定律求出小车的末动量,然后可以求出小车动量的变化量之比,解题时注意正方向的选择.

练习册系列答案
相关题目
7.匀速向东行驶的小车上有两球分别向东、向西同时抛出,抛出时两球的动量大小相等,则( )
| A. | 球抛出后,小车的速度不变 | |
| B. | 球抛出后,小车的速度增加 | |
| C. | 球抛出后,小车的速度减小 | |
| D. | 向西抛出之球的动量变化比向东抛出之球的动量变化大 |
1. 如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿X轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿X轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
 如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿X轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿X轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )| A. | 只能沿x轴正方向 | B. | 可能在xOy平面内,大小为$\frac{2F}{lL}$ | ||
| C. | 可能在zOy平面内,大小为$\frac{2F}{lL}$ | D. | 可能在xOy平面内,大小为$\frac{4F}{IL}$ |

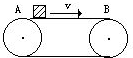 如图所示,绷紧的传送带始终保持着大小为v=4m/s的速度水平匀速运动.一质量m=1kg的小物块无初速地放到皮带A处,物块与皮带间的滑动动摩擦因数μ=0.2,A、B之间距离s=6m.求物块
如图所示,绷紧的传送带始终保持着大小为v=4m/s的速度水平匀速运动.一质量m=1kg的小物块无初速地放到皮带A处,物块与皮带间的滑动动摩擦因数μ=0.2,A、B之间距离s=6m.求物块 弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.2s时,振子速度第一次变为-v;在t=0.5s时,振子速度第二次变为-v.
弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.2s时,振子速度第一次变为-v;在t=0.5s时,振子速度第二次变为-v. 如图甲所示,螺线管匝数n=1500匝,横截面积S=20cm2,其导线电阻r=1.5Ω,回路电阻R1=3.5Ω,R2=25Ω,穿过螺线管的磁场方向从右向左为正,磁感应强度B与t关系为图乙所示的规律变化.则R2的功率为1W,B点的电势为:-5V.
如图甲所示,螺线管匝数n=1500匝,横截面积S=20cm2,其导线电阻r=1.5Ω,回路电阻R1=3.5Ω,R2=25Ω,穿过螺线管的磁场方向从右向左为正,磁感应强度B与t关系为图乙所示的规律变化.则R2的功率为1W,B点的电势为:-5V.