题目内容
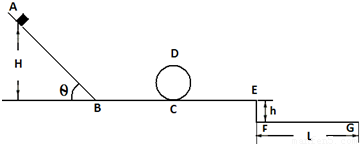
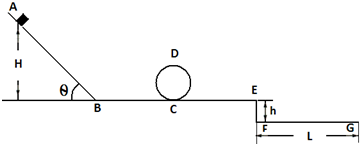
如图所示,某同学仿照“过山车”轨道为一个质量m=0.1kg小滑块设计了轨道.AB为一较长的斜面轨道,与小滑块间的动摩擦因数?=0.2,其它轨道光滑.AB轨道与水平轨道BC成θ=45°,且与BC平滑连接(不计通过B点时的动能损失).小滑块从AB轨道高H=1m处由静止滑下,滑入轨道BC,后从C点进入半径R=0.2m 圆形轨道内侧,转动一周后从C点滑出,再沿水平轨道CE继续运动,最后从E点飞出,落入水平轨道下方h=0.2m的浅槽FG中,浅槽的高度不计,长度L=1.0m. g取10m/s2,小滑块在运动过程中可视为质点.
(1)小滑块到达斜面底端B时速度大小
(2)小滑块到达圆轨道最高点D时对轨道的压力大小
(3)若要小滑块按设计要求完成全部运动,该同学无初速释放小滑块的初始高度应
满足怎样的条件?

(1)小滑块到达斜面底端B时速度大小
(2)小滑块到达圆轨道最高点D时对轨道的压力大小
(3)若要小滑块按设计要求完成全部运动,该同学无初速释放小滑块的初始高度应
满足怎样的条件?
(1)小球从A到B的过程中,由动能定理可得
mgH-μmgcosθ×
=
mvB2
得 VB=4m/s
(2)小球到D时,从释放点到D点由动能定理可得:
mg(H-2R)-μmgcosθ×
=
mvD2
在最高点,轨道对球向下的支持力为N,有
N+mg=
得 N=3N
由牛顿第三定律知,滑块经D点时对轨道的压力大小为N′=3N
(3)设小球恰可以到达圆轨道的最高点,对应的高度为H1,
由圆周运动的规律可知,最高点时的速度vD2
vD2=
mg(H1-2R)-μmgcosθ×
=
mvD22
得H1=0.625m
设小球恰可以到达槽右端,对应的高度为H2
因为t=
所以vE=
=
小球从A到E的过程中,由动能定理:
mgH2-μmgcosθ×
=
mvE2
得:H2=
m=1.5625m
故释放小球的高度范围为:
0.625m≤H≤1.5625m.
答:(1)小滑块到达斜面底端B时速度大小为4m/s.
(2)小滑块到达圆轨道最高点D时对轨道的压力大小为3N.
(3)若要小滑块按设计要求完成全部运动,该同学无初速释放小滑块的初始高度H范围为:0.625m≤H≤1.5625m.
mgH-μmgcosθ×
| H |
| sinθ |
| 1 |
| 2 |
得 VB=4m/s
(2)小球到D时,从释放点到D点由动能定理可得:
mg(H-2R)-μmgcosθ×
| H |
| sinθ |
| 1 |
| 2 |
在最高点,轨道对球向下的支持力为N,有
N+mg=
| mvD2 |
| R |
得 N=3N
由牛顿第三定律知,滑块经D点时对轨道的压力大小为N′=3N
(3)设小球恰可以到达圆轨道的最高点,对应的高度为H1,
由圆周运动的规律可知,最高点时的速度vD2
vD2=
| gR |
mg(H1-2R)-μmgcosθ×
| H1 |
| sinθ |
| 1 |
| 2 |
得H1=0.625m
设小球恰可以到达槽右端,对应的高度为H2
因为t=
|
所以vE=
| L |
| t |
| L | ||||
|
小球从A到E的过程中,由动能定理:
mgH2-μmgcosθ×
| H2 |
| sinθ |
| 1 |
| 2 |
得:H2=
| 25 |
| 16 |
故释放小球的高度范围为:
0.625m≤H≤1.5625m.
答:(1)小滑块到达斜面底端B时速度大小为4m/s.
(2)小滑块到达圆轨道最高点D时对轨道的压力大小为3N.
(3)若要小滑块按设计要求完成全部运动,该同学无初速释放小滑块的初始高度H范围为:0.625m≤H≤1.5625m.

练习册系列答案
相关题目
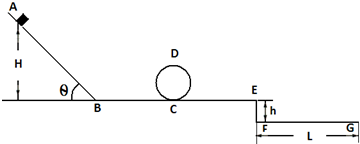
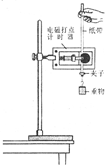 某同学仿照“探究小车速度随时间变化的规律”这一实验,利用如图所示的装置测量重物做自由落体运动的加速度.
某同学仿照“探究小车速度随时间变化的规律”这一实验,利用如图所示的装置测量重物做自由落体运动的加速度.