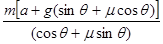题目内容
质量为m的三角形木楔A置于倾角为θ的固定斜面上，它与斜面间的动摩擦因数为μ，一水平力F作用在木楔A的竖直平面上．在力F的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的大小为
．
| mgsinθ+μmgcosθ+ma |
| cosθ-μsinθ |
| mgsinθ+μmgcosθ+ma |
| cosθ-μsinθ |
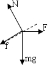
分析：对三角形木楔进行受力分析，运用正交分解，在沿斜面方向上有合力，在垂直于斜面方向上合力等于0，根据牛顿第二定律列出表达式进行求解．
解答：解：沿斜面方向和垂直于斜面方向进行正交分解，根据牛顿第二定律有：
Fcosθ-mgsinθ-f=ma
N=mgcosθ+Fsinθ
f=μN
联立三式得，F=
故本题答案为：
．
Fcosθ-mgsinθ-f=ma
N=mgcosθ+Fsinθ
f=μN
联立三式得，F=
| mgsinθ+μmgcosθ+ma |
| cosθ-μsinθ |
故本题答案为：
| mgsinθ+μmgcosθ+ma |
| cosθ-μsinθ |
点评：解决本题的关键正确画出受力分析图，然后运用正交分解，根据牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示，质量为m的三角形木楔A置于倾角为θ的固定斜面上，它与斜面间的动摩擦因数为μ，一水平力F作用在木楔A的竖直平面上．在力F的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的大小为（ ）
的固定斜面上，它与斜面间的动摩擦因数为
，一水平力F作用在木楔A的竖直平面上，在力F的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的大小为 ( )
B．
D．
B．
D．