题目内容
13.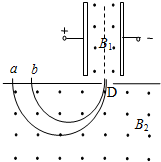 如图所示,电容器两极板之间的距离为d,板间电压为U,极板间的匀强磁场的磁感应强度为B1,一束电荷量相同的带正电的粒子沿图示虚线方向射入电容器,沿直线穿过电容器后从D缝进入另一磁感应强度为B2的匀强磁场,结果分别垂直打在a、b两点,两点间距离为△R.设粒子所带电量为q,且不计粒子所受重力,求打在a、b两点的粒子的质量之差.
如图所示,电容器两极板之间的距离为d,板间电压为U,极板间的匀强磁场的磁感应强度为B1,一束电荷量相同的带正电的粒子沿图示虚线方向射入电容器,沿直线穿过电容器后从D缝进入另一磁感应强度为B2的匀强磁场,结果分别垂直打在a、b两点,两点间距离为△R.设粒子所带电量为q,且不计粒子所受重力,求打在a、b两点的粒子的质量之差.
分析 带电粒子在电容器两极板间所受的电场力和洛伦兹力平衡,做匀速直线运动,进入磁场B2后做匀速圆周运动,根据轨道半径之差,运用洛伦兹力提供向心力求出粒子的质量差.
解答 解:带电粒子在电容器中受力平衡有:qvB1=qE.
又 U=Ed
解得 v=$\frac{U}{d{B}_{1}}$
粒子进入磁场B2后做匀速圆周运动,由洛伦兹力充当向心力,则有
qvB2=m$\frac{{v}^{2}}{R}$
解得 R=$\frac{mU}{qd{B}_{1}{B}_{2}}$
两个粒子的电荷量相等,质量不等.有△R=2(R1-R2)=$\frac{2△mU}{qd{B}_{1}{B}_{2}}$
所以粒子的质量之差△m=$\frac{△Rqd{B}_{1}{B}_{2}}{2U}$
答:打在a、b两点的粒子的质量之差是$\frac{△Rqd{B}_{1}{B}_{2}}{2U}$.
点评 解决本题的关键知道从速度选择器进入偏转磁场,速度相同.以及知道在偏转磁场中的半径与电荷的比荷有关,同位素,电量相同,质量不同,偏转的半径就不同.

练习册系列答案
相关题目
4. 用15cm的细线将质量为8×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为2×104N/C的匀强电场时,小球偏转37°后处在静止状态.下列分析正确的是( )
用15cm的细线将质量为8×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为2×104N/C的匀强电场时,小球偏转37°后处在静止状态.下列分析正确的是( )
 用15cm的细线将质量为8×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为2×104N/C的匀强电场时,小球偏转37°后处在静止状态.下列分析正确的是( )
用15cm的细线将质量为8×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为2×104N/C的匀强电场时,小球偏转37°后处在静止状态.下列分析正确的是( )| A. | 小球带负电 | |
| B. | 小球静止后把悬线烧断,则小球在电场中将作匀加速直线运动 | |
| C. | 小球只受两个力,分别是重力和电场力 | |
| D. | 小球的电荷量为3×10-6 C |
8.质子(p)和α粒子(氦原子核)其质量之比为1:4,电荷量之比为1:2,它们以相同的速率在同一匀强磁场中做匀速圆周运动,轨道半径分别为Rp和Rα,周期分别为Tp和Tα.则下列选项正确的是( )
| A. | Rp:Rα=1:2,Tp:Tα=1:2 | B. | Rp:Rα=1:1,Tp:Tα=1:1 | ||
| C. | Rp:Rα=1:1,Tp:Tα=1:2 | D. | Rp:Rα=1:2,Tp:Tα=1:1 |
5. 一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )
一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )
 一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )
一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )| A. | t=0.5s时离原点最远 | B. | t=1s时离原点最远 | ||
| C. | t=1s时回到原点 | D. | t=2s时回到原点 |


 如图为平面直角坐标系xoy,第一象限有一射线op与x轴成θ1=30°角,第一象限内射线op与y轴之间有垂直纸面向里的匀强磁场B1(大小未知).第二象限内有匀强电场,与y轴负方向成θ2=30°角斜向下,第四象限内有垂直纸面向里的匀强磁场,磁感应强度大小为B2,第二象限有一点A,坐标为(-L,$\sqrt{3}$L),某带电粒子质量为m,电荷量为+q,自A点以某一初速度垂直电场方向射出,后经过坐标原点O进入第四象限的匀强磁场中,已知经过O点时速度大小为v,沿y轴负方向,y轴处于磁场中,不计粒子重力,求:
如图为平面直角坐标系xoy,第一象限有一射线op与x轴成θ1=30°角,第一象限内射线op与y轴之间有垂直纸面向里的匀强磁场B1(大小未知).第二象限内有匀强电场,与y轴负方向成θ2=30°角斜向下,第四象限内有垂直纸面向里的匀强磁场,磁感应强度大小为B2,第二象限有一点A,坐标为(-L,$\sqrt{3}$L),某带电粒子质量为m,电荷量为+q,自A点以某一初速度垂直电场方向射出,后经过坐标原点O进入第四象限的匀强磁场中,已知经过O点时速度大小为v,沿y轴负方向,y轴处于磁场中,不计粒子重力,求: