题目内容
 一质量为M=6kg、带电量为q=-0.1C的小球P自动摩擦因数μ=0.5、倾角θ=53°的粗糙斜面顶端静止开始滑下,斜面高h=6.0m,斜面底端通过一段光滑小圆弧与一光滑水平面相连.整个装置处在水平向右的匀强电场中,场强E=200N/C,忽略小球在连接处的能量损失,当小球运动到水平面时,立即撤去电场.水平面上有另一与P球一摸一样的小球Q,小球Q不带电,且Q与轻质绝缘弹簧相连接.如图所示,设Q静止,P运动到水平面与弹簧发生碰撞.(sin53°=0.8,cos53°=0.6,g=10m/s2.)(水平面小球运动速度满足mAVA+mBVB=mAvA′+mBVB′)
一质量为M=6kg、带电量为q=-0.1C的小球P自动摩擦因数μ=0.5、倾角θ=53°的粗糙斜面顶端静止开始滑下,斜面高h=6.0m,斜面底端通过一段光滑小圆弧与一光滑水平面相连.整个装置处在水平向右的匀强电场中,场强E=200N/C,忽略小球在连接处的能量损失,当小球运动到水平面时,立即撤去电场.水平面上有另一与P球一摸一样的小球Q,小球Q不带电,且Q与轻质绝缘弹簧相连接.如图所示,设Q静止,P运动到水平面与弹簧发生碰撞.(sin53°=0.8,cos53°=0.6,g=10m/s2.)(水平面小球运动速度满足mAVA+mBVB=mAvA′+mBVB′)(1)在整个过程中,P球电势能增加多少?
(2)小球P运动到水平面时的速度大小.
(3)在整个过程中,弹簧具有最大弹性势能为多少?
分析:(1)实际上,P球电势能的改变量是电场力沿电场线做功决定的,即△Eq电=△W电,电势能的改变量转化为动能的改变量;
(2)小球在运动过程中,根据动能定理,即可确定P运动到水平面时的速度大小;
(3)当两球碰撞时小球P的电性对小球Q无影响,静电力只在它们(两小球与弹簧构成的整体)作用,故用动量定理将不必考虑此力.可以用动量的知识考虑,当两个小球共同运动达到同速时,Ep弹最大,从而即可求解.
(2)小球在运动过程中,根据动能定理,即可确定P运动到水平面时的速度大小;
(3)当两球碰撞时小球P的电性对小球Q无影响,静电力只在它们(两小球与弹簧构成的整体)作用,故用动量定理将不必考虑此力.可以用动量的知识考虑,当两个小球共同运动达到同速时,Ep弹最大,从而即可求解.
解答:解:(1)设在整个过程中,P球电势能增加量为E电,d为斜面底部的长度,则有:
d=
=
m=4.5m
得:△Ep电=△W电=eqd=200×0.1×4.5=90J
(2)设:小球P运动到水平面时的速度大小为v,小球在斜面上所受的摩擦力为f,斜面长为L,则有:
f=uMgcos53°=0.5×6×10×0.8N=24N
L=
=
m=7.5m
用动能定理可知:
Mgh-eqd-fL=
mv2-0
6×10×6-200×0.1×4.5-24×7.5=
Mv2
v=
m/s
(3)设:弹簧具有最大弹性势能为Ep弹,两小球达到同速时的速度为V′,
当小球到达水平面上时,其只做匀速运动,用动量定理有:
MV+0=(M+M)V′
解答:V′=
m/s
小球P到达水平面的动能最终转化成弹簧的弹性势能和两个小球的动能为:
MV2=Ep弹+2(
MV′2)
Ep弹=90-45=45J
答:(1)在整个过程中,P球电势能增加90J;
(2)小球P运动到水平面时的速度大小
m/s;
(3)在整个过程中,弹簧具有最大弹性势能为45J.
d=
| h |
| tan53° |
| 6 | ||
|
得:△Ep电=△W电=eqd=200×0.1×4.5=90J
(2)设:小球P运动到水平面时的速度大小为v,小球在斜面上所受的摩擦力为f,斜面长为L,则有:
f=uMgcos53°=0.5×6×10×0.8N=24N
L=
| h |
| sin53° |
| 6 |
| 0.8 |
用动能定理可知:
Mgh-eqd-fL=
| 1 |
| 2 |
6×10×6-200×0.1×4.5-24×7.5=
| 1 |
| 2 |
v=
| 30 |
(3)设:弹簧具有最大弹性势能为Ep弹,两小球达到同速时的速度为V′,
当小球到达水平面上时,其只做匀速运动,用动量定理有:
MV+0=(M+M)V′
解答:V′=
| ||
| 2 |
小球P到达水平面的动能最终转化成弹簧的弹性势能和两个小球的动能为:
| 1 |
| 2 |
| 1 |
| 2 |
Ep弹=90-45=45J
答:(1)在整个过程中,P球电势能增加90J;
(2)小球P运动到水平面时的速度大小
| 30 |
(3)在整个过程中,弹簧具有最大弹性势能为45J.
点评:考查电场力做功导致电势能变化的应用,掌握动能定理与动量定理的应用,注意动能定理中功的正负,动量定理中矢量的方向性,同时运用能量守恒定律来巧妙解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
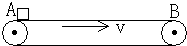 在机场、海港、粮库,常用水平输送带运送旅客、货物、和粮食等,右图为一水平传送带装置示意图,绷紧的传送带A、B始终保持v=2m/s的恒定速率运行;一质量为m=6kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.2,AB间的距离l=4m,g取10m/s2.
在机场、海港、粮库,常用水平输送带运送旅客、货物、和粮食等,右图为一水平传送带装置示意图,绷紧的传送带A、B始终保持v=2m/s的恒定速率运行;一质量为m=6kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.2,AB间的距离l=4m,g取10m/s2.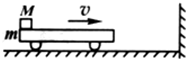 如图所示,水平平板小车质量为m=2kg,其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:
如图所示,水平平板小车质量为m=2kg,其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求: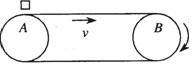
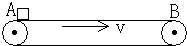 在机场、海港、粮库,常用水平输送带运送旅客、货物、和粮食等,右图为一水平传送带装置示意图,绷紧的传送带A、B始终保持v=2m/s的恒定速率运行;一质量为m=6kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.2,AB间的距离l=4m,g取10m/s2.
在机场、海港、粮库,常用水平输送带运送旅客、货物、和粮食等,右图为一水平传送带装置示意图,绷紧的传送带A、B始终保持v=2m/s的恒定速率运行;一质量为m=6kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.2,AB间的距离l=4m,g取10m/s2.