题目内容
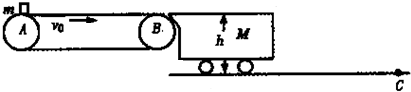
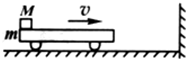 如图所示,水平平板小车质量为m=2kg,其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:
如图所示,水平平板小车质量为m=2kg,其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:①欲使M不从小车上落下,小车至少多长?
②第一次反弹后到最终状态,小车运动的总路程.(小车与水平面的摩擦不计,g=10m/s2 )
分析:(1)由于 m>M,两者以共同速度与墙相碰后,物块的动量大小比车的动量大,由于滑动摩擦力的作用,两者必会又以共同速度再次与墙相碰,由能量转化和守恒定律求解.
(2)对物块与车由动量守恒和运动学公式列出等式求解.
(2)对物块与车由动量守恒和运动学公式列出等式求解.
解答:解:①取平板车与铁块为研究系统,由M>m,系统每次与墙碰后m反向时,M仍以原来速度向右运动,系统总动量向右,故会多次反复与墙碰撞,每次碰后M都要相对m向右运动,直到二者停在墙边,碰撞不损失机械能,系统的动能全在M相对m滑动时转化为内能.设M相对m 滑动的距离为s,则有:
μMgs=
(m+M)v2
解得:s=
=
m
欲便M不从小车上落下,则L≥s,故小车长为:L≥
m
②小车第一次反弹向左以10m/s的速度做减速运动,直到速度为零,其加速度大小为:a=
=15m/s2
故小车第一次向左的最大位移为:s1=
代入数据得:s1=
m
设小车第n-1次碰前速度为vn-1,第n次碰前速度为vn,则第n-1次碰后到第n次碰前过程动量守恒,有:Mvn-1-mvn-1=(m+M)vn,
所以有:vn=
vn-1=
vn-1
第n-1次碰后小车反弹速度为vn-1,向左减速的最大位移为:sn-1=
随后向右加速距离为:s′=
显然有:vn<vn-1,s′<sn-1
所以在碰前有相等速度,第n次碰后向左运动的最大位移为:
sn=
所以有:
=
=
,
即成等比数列.小车运动的总路程为:
s=2(s1+s2+s3+…+sn…)=
=
=
m
答:①欲使M不从小车上落下,小车至少
m.
②第一次反弹后到最终状态,小车运动的总路程
m.
μMgs=
| 1 |
| 2 |
解得:s=
| (m+M)v2 |
| 2μMg |
| 40 |
| 3 |
欲便M不从小车上落下,则L≥s,故小车长为:L≥
| 40 |
| 3 |
②小车第一次反弹向左以10m/s的速度做减速运动,直到速度为零,其加速度大小为:a=
| μMg |
| m |
故小车第一次向左的最大位移为:s1=
| v02 |
| 2a |
代入数据得:s1=
| 10 |
| 3 |
设小车第n-1次碰前速度为vn-1,第n次碰前速度为vn,则第n-1次碰后到第n次碰前过程动量守恒,有:Mvn-1-mvn-1=(m+M)vn,
所以有:vn=
| M-m |
| M+m |
| 1 |
| 2 |
第n-1次碰后小车反弹速度为vn-1,向左减速的最大位移为:sn-1=
| vn-12 |
| 2a |
随后向右加速距离为:s′=
| vn2 |
| 2a |
显然有:vn<vn-1,s′<sn-1
所以在碰前有相等速度,第n次碰后向左运动的最大位移为:
sn=
| vn2 |
| 2a |
所以有:
| sn |
| sn-1 |
| vn2 |
| vn-12 |
| 1 |
| 4 |
即成等比数列.小车运动的总路程为:
s=2(s1+s2+s3+…+sn…)=
| 2s1 | ||
1-
|
2×
| ||
1-
|
| 80 |
| 9 |
答:①欲使M不从小车上落下,小车至少
| 40 |
| 3 |
②第一次反弹后到最终状态,小车运动的总路程
| 80 |
| 9 |
点评:本题关键是根据动量守恒定律、能量守恒列式求解,也可以根据牛顿第二定律和运动学公式列式联立求解,同时要注意数学知识在物理中的应用.

练习册系列答案
相关题目
 如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求:
如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求: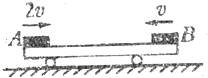 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求: 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求: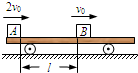 如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求:
如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求: