题目内容
14.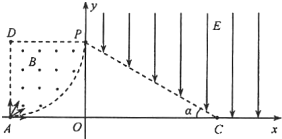 在如图的xOy坐标系中.A(-L,0)、C是x轴上的两点,P点的坐标为(0,L).在第二象限内以D(-L,L)为圆心、L为半径的$\frac{1}{4}$圆形区域内,分布着方向垂直xOy平面向外、磁感应强度大小为B的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场.现有大量质量为m、电荷量为+q的相同粒子,从A点平行xOy平面以相同速率、沿不同方向射向磁场区域,其中沿AD方向射入的粒子恰好从P点
在如图的xOy坐标系中.A(-L,0)、C是x轴上的两点,P点的坐标为(0,L).在第二象限内以D(-L,L)为圆心、L为半径的$\frac{1}{4}$圆形区域内,分布着方向垂直xOy平面向外、磁感应强度大小为B的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场.现有大量质量为m、电荷量为+q的相同粒子,从A点平行xOy平面以相同速率、沿不同方向射向磁场区域,其中沿AD方向射入的粒子恰好从P点进入电场,经电场后恰好通过C点.已知a=30°,不考虑粒子间的相互作用及其重力,求:
(1)电场强度的大小;
(2)x正半袖上有粒子穿越的区间.
分析 (1)带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直,进而电场后做类平抛运动,根据牛顿第二定律结合平抛运动基本公式求解电场强度;
(2)设粒子的速度方向与x轴正方向的夹角为θ,粒子从F点射出磁场,由于r=L,故四边形ADFO′为菱形,带电粒子离开磁场时,速度方向沿x轴正方向,根据几何关系结合平抛运动基本公式求出粒子到达x轴的坐标的表达式,从而求出x的范围.
解答  解:(1)带电粒子在磁场中做匀速圆周运动,设半径为r,粒子初速度为v0,
解:(1)带电粒子在磁场中做匀速圆周运动,设半径为r,粒子初速度为v0,
则$Bq{v}_{0}=m\frac{{{v}_{0}}^{2}}{r}$,
由几何关系得:r=L,
沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直,
设在电场中运动的时间为t0,电场强度为E,则
qE=ma,
$\frac{L}{tanα}={v}_{0}{t}_{0}$,
L=$\frac{1}{2}a{{t}_{0}}^{2}$
解得:E=$\frac{2q{B}^{2}L}{3m}$
(2)若粒子的速度方向与x轴正方向的夹角为θ,粒子从F点射出磁场,由于r=L,故四边形ADFO′为菱形,
O′F平行AD,vF⊥O′F,
带电粒子离开磁场时,速度方向沿x轴正方向,则有:
yF=L(1-cosθ),
粒子从F′通过PC,则
${x}_{F′}=\frac{L-{y}_{F}}{tanα}$
粒子在电场中运动的时间为t,从C′通过x轴离开电场,沿x轴方向的位移为x,
x=v0t,${y}_{F}=\frac{1}{2}a{t}^{2}$,
粒子到达x轴的坐标为xC′,xC′=xF′+x
${x}_{C′}=\sqrt{3}L(cosθ+\sqrt{1-cosθ})$(0<θ≤90°)
当θ=90°时,xC′的最小值${x}_{min}=\sqrt{3}L$,
当$cosθ=\frac{3}{4}$时,xC′的最大值${x}_{max}=\frac{5\sqrt{3}}{4}L$
所以x正半袖上有粒子穿越的区间为$\sqrt{3}L≤{x}_{C′}≤\frac{5\sqrt{3}}{4}L$
答:(1)电场强度的大小为$\frac{2q{B}^{2}L}{3m}$;
(2)x正半袖上有粒子穿越的区间为$\sqrt{3}L≤{x}_{C′}≤\frac{5\sqrt{3}}{4}L$.
点评 带电粒子在组合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况,再选择合适方法处理.对于匀变速曲线运动,常常运用运动的分解法,将其分解为两个直线的合成,由牛顿第二定律和运动学公式结合求解;对于磁场中圆周运动,要正确画出轨迹,由几何知识求解半径.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 如图是机场的安检人员用手持金属探测器检查乘客的情景.探测线圈内通有交变电流,能产生迅速变化的磁场.当探测线圈靠近金属物体时,这个磁场能在金属物体内部能产生涡电流,涡电流又会产生磁场,倒过来影响原来的磁场.如果能检测出这种变化,就可以判定探测线圈下面有金属物体了.以下用电器与金属探测器工作原理相似--利用涡流的是( )
如图是机场的安检人员用手持金属探测器检查乘客的情景.探测线圈内通有交变电流,能产生迅速变化的磁场.当探测线圈靠近金属物体时,这个磁场能在金属物体内部能产生涡电流,涡电流又会产生磁场,倒过来影响原来的磁场.如果能检测出这种变化,就可以判定探测线圈下面有金属物体了.以下用电器与金属探测器工作原理相似--利用涡流的是( )| A. |  变压器 | B. |  日光灯 | C. |  电磁炉 | D. |  直流电动机 |
| A. | 斜槽轨道末端必须水平 | B. | 轨道必须光滑 | ||
| C. | 每次都要平衡摩擦力 | D. | 小球每次应从斜槽同一高度释放 |
| A. | αA=αB,FA=FB | B. | αA=αB,FA>FB | C. | αA>αB,FA=FB | D. | αA>αB,FA>FB |
| A. | 声波的干涉现象 | B. | 声波的衍射现象 | ||
| C. | 声波的多普勒效应 | D. | 声波的反射现象 |
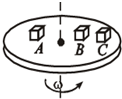 如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )
如图所示,A、B、C三个物体放在水平旋转的圆盘上,保持与圆盘相对静止,三个物体与圆盘的动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴距离为R,C离轴为2R.若最大静摩擦力可认为等于滑动摩擦力,则( )| A. | 每个物体均受重力、支持力、静摩擦力、向心力四个力作用 | |
| B. | A的向心加速度大于B的向心加速度 | |
| C. | B和C所受摩擦力相等 | |
| D. | 若逐渐增大圆盘转速,C比B先滑动,A和B同时滑动 |
 如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s.
如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s. 如图所示,竖直平面内有间距l=40cm、足够长的平行直导轨,导轨上端连接一开关S.长度恰好等于导轨间距的导体棒ab与导轨接触良好且无摩擦,导体棒ab的电阻R=0.40Ω,质量m=0.20kg.导轨电阻不计,整个装置处于与导轨平面垂直的水平匀强磁场中,磁场的磁感强度B=0.50T,方向垂直纸面向里.空气阻力可忽略不计,取重力加速度g=10m/s2.
如图所示,竖直平面内有间距l=40cm、足够长的平行直导轨,导轨上端连接一开关S.长度恰好等于导轨间距的导体棒ab与导轨接触良好且无摩擦,导体棒ab的电阻R=0.40Ω,质量m=0.20kg.导轨电阻不计,整个装置处于与导轨平面垂直的水平匀强磁场中,磁场的磁感强度B=0.50T,方向垂直纸面向里.空气阻力可忽略不计,取重力加速度g=10m/s2.