题目内容
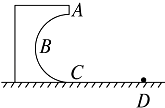
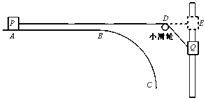
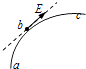
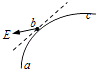
【题目】如图,光滑圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一小球从水平桌面的边缘P点以速度v0向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道,OA与竖直方向的夹角为θ1 , PA与竖直方向的夹角为θ2 . 下列说法正确的是( )
A.tan θ1cot θ2=2
B.tan θ1tan θ2=2
C.从P到C过程小球机械能减少
D.小球从C斜抛出去达到最高点时,与P等高且速度也等于v0
【答案】B,D
【解析】解:AB、小球恰好能沿圆弧切线方向进入圆弧轨道,知道速度的方向与OA垂直,速度与水平方向的夹角为θ1 , 位移与水平方向的夹角为θ2 .
在A点,有 tanθ1= ![]() ,又 tanθ2=
,又 tanθ2= ![]() =
= ![]() =
= ![]() ,则得 tan θ1tan θ2=2.故A错误,B正确.
,则得 tan θ1tan θ2=2.故A错误,B正确.
C、从P到C的过程中,只有重力做功,小球的机械能守恒.故C错误.
D、根据运动的对称性,知从C斜抛出去达到最高点时,与P等高且速度也等于v0 . 故D正确.
故选:BD
【考点精析】掌握机械能守恒及其条件是解答本题的根本,需要知道在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变.

练习册系列答案
相关题目