��Ŀ����
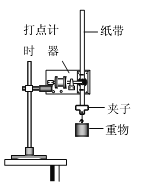
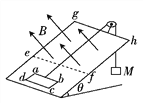
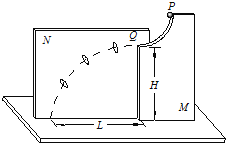
����Ŀ������٤����ʱ����ʾƽ���˶��ķ���������ͼʾ��ʵ��װ�ã�ͼ��ˮƽ���õĵװ�����ֱ�ع̶���M���N�壮M ���ϲ���һ�뾶ΪR��![]() Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ����������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����
Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ����������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����
��1��С��Q��ʱ���ٶȴ�С��
��2��С���˶���Q��ʱ�Թ����ѹ����С��
��3��С��˷�Ħ�������Ĺ���
���𰸡���1��С��Q��ʱ���ٶȴ�СΪL![]() ��
��
��2��С���˶���Q��ʱ�Թ����ѹ����СΪmg+![]() ��
��
��3��С��˷�Ħ�������Ĺ�ΪmgR��![]() ��
��
���������⣺��1����ƽ���˶����ɿ�֪��
ˮƽ�������У�L=vt��
��ֱ�������У�H=![]() gt2��
gt2��
��ã�v=![]() =L
=L![]()
��2��С����Q������mg�����֧����F֧�����׳����������ţ�ٵڶ����ɣ�F֧��mg=m![]()
��ã�F֧=mg+![]()
��ţ�ٵ������ɣ�Fѹ=F֧=mg+![]()
��3����P����Q��Ĺ��̣�Ӧ�ö��ܶ����У�mgR+Wf=![]() mv2��0
mv2��0
��ã�Wf=![]() ��mgR
��mgR
W��f=mgR��![]()
�𣺣�1��С��Q��ʱ���ٶȴ�СΪL![]() ��
��
��2��С���˶���Q��ʱ�Թ����ѹ����СΪmg+![]() ��
��
��3��С��˷�Ħ�������Ĺ�ΪmgR��![]() ��
��