题目内容
 (2007?上海)如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为E0的带电粒子从a点沿ab方向进入电场,不计重力.
(2007?上海)如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为E0的带电粒子从a点沿ab方向进入电场,不计重力.(1)若粒子从c点离开电场,求电场强度的大小和粒子离开电场时的动能.
(2)若粒子离开电场时动能为EK′,求电场强度的大小?
分析:(1)将运动沿着水平和竖直方向正交分解,运用牛顿运动定律、运动学公式和动能定理列式求解;
(2)粒子在ab方向上作匀速运动;粒子在ad方向上做初速度为0的匀加速运动;运用牛顿运动定律、运动学公式和动能定理列式求解.
(2)粒子在ab方向上作匀速运动;粒子在ad方向上做初速度为0的匀加速运动;运用牛顿运动定律、运动学公式和动能定理列式求解.
解答:解:(1)粒子的初动能为,E0=
m
粒子在ab方向上作匀速运动,L=v0t
粒子在ad方向上做初速度为0的匀加速运动,L=
at2
根据牛顿第二定律,a=
所以E=
根据动能定理,有
qEL=Ekt-E0
所以
Ekt=qEL+E0=5E0.
即电场强度的大小为
,粒子离开电场时的动能为5E0.
(2)根据牛顿第二定律,有
qE=ma ①
沿初速度方向做匀速运动,有
x=v0t ②
沿电场方向的分位移为
y=
at2 ③
根据动能定理,有
qEy=EK′-E0 ④
当带电粒子从bc边飞出时,x=L,y<L,由①②③④式联立解得
E=
=
当带电粒子从cd边飞出时,y=L,x<L,由①②③④式联立解得
E=
即当带电粒子从bc边飞出时电场强度为E=
;当带电粒子从cd边飞出时电场强度为
.
| 1 |
| 2 |
| v | 2 0 |
粒子在ab方向上作匀速运动,L=v0t
粒子在ad方向上做初速度为0的匀加速运动,L=
| 1 |
| 2 |
根据牛顿第二定律,a=
| qE |
| m |
所以E=
| 4E0 |
| qL |
根据动能定理,有
qEL=Ekt-E0
所以
Ekt=qEL+E0=5E0.
即电场强度的大小为
| 4E0 |
| qL |
(2)根据牛顿第二定律,有
qE=ma ①
沿初速度方向做匀速运动,有
x=v0t ②
沿电场方向的分位移为
y=
| 1 |
| 2 |
根据动能定理,有
qEy=EK′-E0 ④
当带电粒子从bc边飞出时,x=L,y<L,由①②③④式联立解得
E=
v0
| ||
| qL |
| ||
| qL |
当带电粒子从cd边飞出时,y=L,x<L,由①②③④式联立解得
E=
| Ek′-E0 |
| qL |
即当带电粒子从bc边飞出时电场强度为E=
| ||
| qL |
| Ek′-E0 |
| qL |
点评:本题关键将带电粒子的运动沿初速度方向和电场方向进行正交分解,然后根据牛顿第二定律和运动学公式列式求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 (2007?上海)如图所示,AB两端接直流稳压电源,UAB=100V,R0=40Ω,滑动变阻器总电阻R=20Ω,当滑动片处于变阻器中点时,C、D两端电压UCD为多少?通过电阻R0的电流为多少?
(2007?上海)如图所示,AB两端接直流稳压电源,UAB=100V,R0=40Ω,滑动变阻器总电阻R=20Ω,当滑动片处于变阻器中点时,C、D两端电压UCD为多少?通过电阻R0的电流为多少? (2007?上海)如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0.开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K,现缓慢加热汽缸内气体,直至399.3K.求:
(2007?上海)如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0.开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K,现缓慢加热汽缸内气体,直至399.3K.求: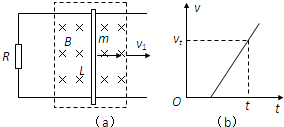 (2007?上海)如图(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为f的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内.
(2007?上海)如图(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为f的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内. (2007?上海)如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(可以认为在斜面上是初速为零的匀加速运动,在水平面上是匀减速运动,重力加速度g=10m/s2)
(2007?上海)如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(可以认为在斜面上是初速为零的匀加速运动,在水平面上是匀减速运动,重力加速度g=10m/s2)