题目内容
8.长度为2m,质量为1kg的木板静止于光滑的水平面上,一个质量也为1kg的木块(可视为质点),与木板之间的动摩擦因数为0.2.要使木块在木板上从左端滑向右端而不至于滑落,则木块的初速度的最大值为( )| A. | 1m/s | B. | 2m/s | C. | 3m/s | D. | 4m/s |
分析 滑块最终不会从木板上掉下的临界情况是滑块滑到最右端时,滑块与木板具有相同速度,根据动量守恒定律及能量守恒定律即可求解最大速度.
解答 解:以木板和木块为研究对象,以向右运动的方向为正方向,根据动量守恒定律得:mv0=(M+m)v
根据能量守恒定律得:fL=$\frac{1}{2}m{v}_{0}-\frac{1}{2}(m+M){v}^{2}$
又因为:f=μmg
代入数据解得v0=4m/s.故ABC错误,D正确.
故选:D.
点评 本题综合运用了动量守恒定律和能量守恒定律,知道该问题的临界情况,以及知道摩擦产生的热量Q=f△s=fL.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
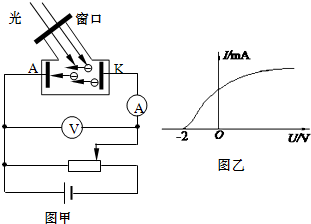
18. 如图所示的电路中,电源内阻一定,电压表和电流表均为理想电表.现使滑动变阻器R的滑片向左滑动一小段距离,测得电压表V1的示数变化大小为△U1,电压表V2的示数变化大小为△U2,电流表A的示数变化大小为△I,对于此过程下列说法正确的是( )
如图所示的电路中,电源内阻一定,电压表和电流表均为理想电表.现使滑动变阻器R的滑片向左滑动一小段距离,测得电压表V1的示数变化大小为△U1,电压表V2的示数变化大小为△U2,电流表A的示数变化大小为△I,对于此过程下列说法正确的是( )
 如图所示的电路中,电源内阻一定,电压表和电流表均为理想电表.现使滑动变阻器R的滑片向左滑动一小段距离,测得电压表V1的示数变化大小为△U1,电压表V2的示数变化大小为△U2,电流表A的示数变化大小为△I,对于此过程下列说法正确的是( )
如图所示的电路中,电源内阻一定,电压表和电流表均为理想电表.现使滑动变阻器R的滑片向左滑动一小段距离,测得电压表V1的示数变化大小为△U1,电压表V2的示数变化大小为△U2,电流表A的示数变化大小为△I,对于此过程下列说法正确的是( )| A. | 通过电阻R1的电流变化量大小等于$\frac{△{U}_{1}}{{R}_{1}}$ | |
| B. | R0两端的电压的变化量大小等于△U1-△U2 | |
| C. | 路端电压的增加量等于△U2 | |
| D. | $\frac{△{U}_{1}}{△I}$为一定值 |
19.下列说法正确的是( )
| A. | 液晶的光学性质具有各向异性 | |
| B. | 空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比 | |
| C. | 小昆虫能在水面上自由走动与表面张力有关 | |
| D. | 玻璃、石墨和金刚石都是晶体,木炭是非晶体 |
20.下列几种情况下力F都对物体做了功:
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
①水平推力F推着质量为m的物体从静止开始在光滑水平面上前进了S;
②水平推力F推着质量为m的物体从静止开始在粗糙水平面上前进了S.
下列关于力F所做的功说法正确的是( )
| A. | ①做功最多 | B. | ②做功最多 | C. | 无法确定 | D. | 做功都相等 |
17.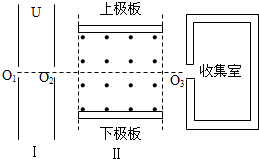 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )| A. | 区域Ⅱ的电场方向竖直向下 | |
| B. | 该装置可筛选出具有特定质量的粒子 | |
| C. | 该装置可筛选出具有特定速度的粒子 | |
| D. | 若射入的粒子电荷量相同,则该装置筛选出的粒子一定具有相同的质量 |
18.用一根细绳连接物体与固定点,如果物体在光滑水平面上做匀速圆周运动时细绳突然断裂,下列说法正确的是( )
| A. | 物体将继续在原来的圆周上运动 | |
| B. | 物体将沿着圆周的切线方向飞出去 | |
| C. | 物体将沿着切线和圆周之间的某一条曲线向远离圆心的方向运动 | |
| D. | 物体将朝着圆心运动 |
 如图所示,竖直平面内有无限长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在磁感应强度B=2T的匀强磁场.完全相同的两根金属杆1和2靠在导轨上,金属杆与导轨等宽且与导轨接触良好,电阻均为r=0.5Ω.将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰做匀速运动(g取10m/s2).
如图所示,竖直平面内有无限长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在磁感应强度B=2T的匀强磁场.完全相同的两根金属杆1和2靠在导轨上,金属杆与导轨等宽且与导轨接触良好,电阻均为r=0.5Ω.将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰做匀速运动(g取10m/s2).