题目内容
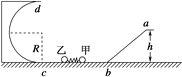
【题目】如图所示,光滑轨道abc固定在竖直平面内,ab倾斜、bc水平,与半径R=0.4 m竖直固定的粗糙半圆形轨道cd在c点平滑连接.可视为质点的小球甲和乙静止在水平轨道上,二者中间压缩有轻质弹簧,弹簧与两小球均不拴接且被锁定.现解除对弹簧的锁定,小球甲在脱离弹簧后恰能沿轨道运动到a处,小球乙在脱离弹簧后沿半圆形轨道恰好能到达最高点d.已知小球甲的质量m1=2 kg,a、b的竖直高度差h=0.45 m,已知小球乙在c点时轨道对其弹力的大小F=100 N,弹簧恢复原长时两小球均在水平轨道上,不计空气阻力,重力加速度g取10 m/s2.求:
(1)小球乙的质量;
(2)小球乙在半圆形轨道上克服摩擦力所做的功.
【答案】(1)1kg(2)8J
【解析】
(1)对小球甲,由机械能守恒定律得
m1gh=![]() m1
m1![]()
对小球甲、乙,由动量守恒定律得
m1v1=m2v2
对小球乙,在c点,由牛顿第二定律得
F-m2g=m2![]()
联立解得
m2=1kg,v2=6m/s或m2=9kg,v2=![]() m/s
m/s
小球乙恰好过d点,有
m2g=m2![]()
解得
vd=![]() =2m/s
=2m/s
由题意vd<v2,所以小球乙的质量
m2=1kg
(2)对小球乙在半圆形轨道上运动的过程中,由动能定理有
2m2gR+Wf=![]() -
-![]()
解得小球乙克服摩擦力所做的功
Wf=8J

练习册系列答案
相关题目