��Ŀ����
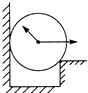
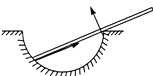
����Ŀ����ͼ��ʾ��һ������ ![]() Բ���Ĵֲڻ���A��������mA=3kg �� ��Բ��������ˮƽ����������P �� ˮƽ����PQ��L=3.75m �� ��ʼʱ��A��ֹ�ڹ⻬ˮƽ���ϣ�����һ����mB=2kg��Сľ��B�ӻ���A���Ҷ���ˮƽ���ٶ�v0=5m/S����A �� Сľ��B�뻬��A֮��Ķ�Ħ��������=0.15��Сľ��B��������A����˲�����Բ�������ϻ�һ�λ����أ�����ֹͣ�ڻ���A�ϣ�
Բ���Ĵֲڻ���A��������mA=3kg �� ��Բ��������ˮƽ����������P �� ˮƽ����PQ��L=3.75m �� ��ʼʱ��A��ֹ�ڹ⻬ˮƽ���ϣ�����һ����mB=2kg��Сľ��B�ӻ���A���Ҷ���ˮƽ���ٶ�v0=5m/S����A �� Сľ��B�뻬��A֮��Ķ�Ħ��������=0.15��Сľ��B��������A����˲�����Բ�������ϻ�һ�λ����أ�����ֹͣ�ڻ���A�ϣ�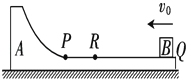
��1����A��B��Ծ�ֹʱ���ٶȴ�С��
��2����B����ͣ��A��ˮƽ�����ϵ�R�㣬P��R���1m �� ��B��Բ�����˶��Ĺ�������Ħ�������������ܣ�
��3����Բ�����ֹ⻬���ҳ�v0��ȷ���������������䣬����Сľ��B�������˶������У��Ƿ��п�����ij��ʱ������Ե��������˶����粻���ܣ�˵�����ɣ�����ܣ������B�����һ������ֲ�����ľ��A��v0ȡֵ��Χ����ȡg=10m/S2 �� ������Ա������ţ�
���𰸡�
��1��
A��Bϵͳ�����غ㣬��B�ij��ٶȷ���Ϊ������
�ɶ����غ㶨�ɵã�mBv0=��mB+mA��v���������ݽ�ã�v=2m/S
��2��
��B��A��Բ�����ֲ���������ΪQ1����A��ˮƽ���ֲ���������ΪQ2��
�������غ㶨�ɵã� ![]() mBv02=
mBv02= ![]() ��mB+mA��v2+Q1+Q2��
��mB+mA��v2+Q1+Q2��
�֣�Q2=��mBg��LQP+LPR�����������ݽ�ã�Q1=0.75J
��3��
��Сľ��B�»���P��ʱ�ٶ�ΪvB��ͬʱA���ٶ�ΪvA��
��B�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�mBv0=mBvB+mAvA��
�������غ㶨�ɵã� ![]() mBv02=
mBv02= ![]() mBvB2+
mBvB2+ ![]() mAvA2+��mBgL��
mAvA2+��mBgL��
�������ݽ�ã�vB2��0.8v0vB+6.75��0.2v02=0��
��vB��������һ��һ��ʱ����ʾB��Բ�����µ��ٶ����ң�
����v0��5.9m/S��B�п�����Ե��������˶���
���B���ղ�����A�����У���mBg2L�� ![]() mBv02=
mBv02= ![]() ��mB+mA����0.4v0��2��
��mB+mA����0.4v0��2��
�������ݽ�ã�v0��6.1m/S����v0��ȡֵ��Χ�ǣ�5.9m/S��v0��6.1m/S
����������1��Сľ��B�ӿ�ʼ�˶�ֱ��A��B��Ծ�ֹ�Ĺ����У�ϵͳˮƽ������������ˮƽ�����϶����غ㣬����ˮƽ�������غ����A��B��Ծ�ֹʱ���ٶȴ�С����2����B����ͣ��A��ˮƽ�����ϵ�R�㣬ϵͳ�Ļ�е�ܼ�С��ת��Ϊϵͳ�����ܣ����������غ㶨�����ϵͳ�ڸ��˶���������Ħ�����������ܣ���3������ϵͳ�Ķ����غ��������Ϸ���B�������һ������ֲ�����ľ��A��v0ȡֵ��Χ��
�����㾫����������Ĺؼ�����������غ㶨�ɵ����֪ʶ�����ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮