题目内容
如图所示,ABCD为固定的水平光滑矩形金属导轨,处在方向竖直向下,磁感应强度为B的匀强磁场中,AB间距为L,左右两端均接有阻值为R的电阻,质量为m、长为L且不计电阻的导体棒MN放在导轨上,与导轨接触良好,并与轻质弹簧组成弹簧振动系统.开始时,弹簧处于自然长度,导体棒MN具有水平向左的初速度v0,经过一段时间,导体棒MN第一次运动到最右端,这一过程中AB间R上产生的焦耳热为Q,则
A.初始时刻棒所受的安培力大小为 |
B.当棒再一次回到初始位置时,AB间电阻的热功率为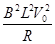 |
C.当棒第一次到达最右端时,弹簧具有的弹性势能为 mv02-2Q mv02-2Q |
D.当棒第一次到达最右端时,弹簧具有的弹性势能为 mv02-6Q mv02-6Q |
AC
解析试题分析:据导体棒切割磁感线产生的电动势E=BLv0,导体棒中经过的电流I=E/R并和并联总电阻R并=R/2,以及导体棒所受安培力F=BIL,得到安培力F= ,所以A选项正确;由于安培力做负功,当导体棒再次回到初始位置时,安培力F’<
,所以A选项正确;由于安培力做负功,当导体棒再次回到初始位置时,安培力F’< ,此时安培力的功率P’<
,此时安培力的功率P’< ,则AB间的电阻热功率也小于
,则AB间的电阻热功率也小于 ,所以B选项错误;当导体棒从初位置到第一次到达最右端时,由动能定理得:-WF-W弹=-mv20/2,而WF=2Q,所以此过程弹簧具有是弹性势能为:E弹=mv20/2-WF= mv20/2-2Q,C选项正确。
,所以B选项错误;当导体棒从初位置到第一次到达最右端时,由动能定理得:-WF-W弹=-mv20/2,而WF=2Q,所以此过程弹簧具有是弹性势能为:E弹=mv20/2-WF= mv20/2-2Q,C选项正确。
考点:本题考查能量守恒定律的应用,热功率的应用。

 阅读快车系列答案
阅读快车系列答案如图是法拉第研制成的世界上第一台发电机模型的原理图。铜盘水平放置,磁场竖直向下穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,从上往下看逆时针匀速转动铜盘,下列说法正确的是
| A.回路中电流大小变化,,方向不变 |
| B.回路中没有磁通量变化,没有电流 |
| C.回路中有大小和方向作周期性变化的电流 |
| D.回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 |
在匀强磁场中有两条平行的金属导轨,磁场方向与导轨平面垂直,导轨上有两条可以沿导轨自由移动的导电棒ab、cd,这两根导电棒的速度分别为v1、v2,如图所示,ab棒上没有感应电流通过,则一定有( )
| A.v1>v2 | B.v1<v2 | C.v1≠v2 | D.v1=v2 |
如图所示,粗糙水平桌面上有一质量为m的铜质矩形线圈.当一竖直放置的条形磁铁从线圈中线AB正上方等高快速经过时,若线圈始终不动,则关于线圈受到的支持力FN及在水平方向运动趋势的正确判断是( )
| A.FN先小于mg后大于mg,运动趋势向左 |
| B.FN先大于mg后小于mg,运动趋势向左 |
| C.FN先小于mg后大于mg,运动趋势向右 |
| D.FN先大于mg后小于mg,运动趋势向右 |
金属杆a b水平放置在某高处,当它被平抛进入方向坚直向上的匀强磁场中时(如图所示),以下说法中正确的是 ( )
| A.运动过程中感应电动势大小不变,且Ua>Ub |
| B.运动过程中感应电动势大小不变,且Ua<Ub |
| C.由于速率不断增大,所以感应电动势不断变大,且Ua>Ub |
| D.由于速率不断增大,所以感应电动势不断变大,且Ua<Ub |








