题目内容
如图甲所示,在xOy平面内存在磁场和电场,磁感应强度和电场强度大小随时间周期性变化,B的变化周期为4t0,E的变化周期为2t0,变化规律分别如图乙和图丙所示.在t=0时刻从O点发射一带负电的粒子(不计重力),初速度大小为v0,方向沿y轴正方向.在x轴上有一点A(图中末标出),坐标为(
,0).若规定垂直纸面向里为磁感应强度的正方向,y轴正方向为电场强度的正方向,v0、t0、B0为已知量,磁感应强度与电场强度的大小满足:
=
;粒子的比荷满足:
=
.求:
(1)在t=
时,粒子的位置坐标;
(2)粒子偏离x轴的最大距离;
(3)粒子运动至A点的时间.

| 48v0t0 |
| π |
| E0 |
| B0 |
| v0 |
| π |
| q |
| m |
| π |
| B0t0 |
(1)在t=
| t0 |
| 2 |
(2)粒子偏离x轴的最大距离;
(3)粒子运动至A点的时间.

分析:根据洛伦兹力提供向心力和周期公式求粒子的坐标;画出粒子运动轨迹,据此求粒子的最大距离;根据左周期性运动的周期,和一个周期内运动的距离求时间.
解答:解:(1)在0~t0时间内,粒子做匀速圆周运动,根据洛伦兹力提供向心力可得:
qBv 0=mr1
=m
得:T=
=2t0r1=
=
则在
时间内转过的圆心角α=
所以在t=
时,粒子的位置坐标为:(
,
)
(2)在t0~2t0时间内,粒子经电场加速后的速度为v,粒子的运动轨迹如图所示
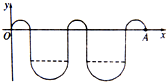 v=v0+
v=v0+
t0=2v0
运动的位移:x=
t0=1.5v0t0
在2t0~3t0时间内粒子做匀速圆周运动,半径:r2=2r1=
故粒子偏离x轴的最大距离:h=x+r2=1.5v0t0+
(3)粒子在xOy平面内做周期性运动的运动周期为4t0
一个周期内向右运动的距离:d=2r1+2r2=
AO间的距离为:
=8d
所以,粒子运动至A点的时间为:t=32t0
答:(1)在t=
时,粒子的位置坐标(
,
);
(2)粒子偏离x轴的最大距离h=x+r2=1.5v0t0+
;
(3)粒子运动至A点的时间32t0.
qBv 0=mr1
| 4π2 |
| T2 |
| ||
| r1 |
得:T=
| 2πm |
| qB0 |
| mv0 |
| qB0 |
| v0t0 |
| π |
则在
| t0 |
| 2 |
| π |
| 2 |
所以在t=
| t0 |
| 2 |
| v0t0 |
| π |
| v0t0 |
| π |
(2)在t0~2t0时间内,粒子经电场加速后的速度为v,粒子的运动轨迹如图所示
 v=v0+
v=v0+| E0q |
| m |
运动的位移:x=
| v0+v |
| 2 |
在2t0~3t0时间内粒子做匀速圆周运动,半径:r2=2r1=
| 2v0t0 |
| π |
故粒子偏离x轴的最大距离:h=x+r2=1.5v0t0+
| 2v0t0 |
| π |
(3)粒子在xOy平面内做周期性运动的运动周期为4t0
一个周期内向右运动的距离:d=2r1+2r2=
| 6v0t0 |
| π |
AO间的距离为:
| 48v0t0 |
| π |
所以,粒子运动至A点的时间为:t=32t0
答:(1)在t=
| t0 |
| 2 |
| v0t0 |
| π |
| v0t0 |
| π |
(2)粒子偏离x轴的最大距离h=x+r2=1.5v0t0+
| 2v0t0 |
| π |
(3)粒子运动至A点的时间32t0.
点评:带电粒子在电场、磁场和重力场等共存的复合场中的运动,其受力情况和运动图景都比较复杂,但其本质是力学问题,应按力学的基本思路,运用力学的基本规律研究和解决此类问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 ;
;
 ;
;